-
При изменении направления обхода контура циркуляция векторного поля изменяет свой знак на обратный:
Этим свойством обладают все криволинейные интегралы второго рода, в том числе и интегралы по замкнутому контуру, поскольку изменение направления касательного вектора l на противоположное влечет за собой изменение знака проекции вектора A на направление l.
-
Если односвязную область, ограниченную контуром L, разбить на две части, границами которых являются контуры L1 и L2, то циркуляция векторного поля A по контуру L равна сумме циркуляций по контурам L1 и L2:
(Справка: Область называется односвязной, если любую лежащую в ней замкнутую кривую можно непрерывной деформацией стянуть в произвольную точку, не выходя за границы области.)
Такое разбиение можно осуществить, выбрав на контуре L любые две точки и соединив их линией AB (как это показано на рисунке 1).
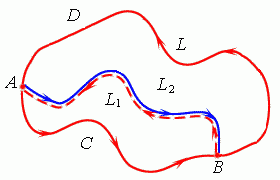Рис. 1. Разбиение замкнутого контура L на две петли.
Действительно, контур L1 включают в себя часть контура L (дугу ACB) и линию BA, тогда как контур L2 состоит из оставшейся части контура L (дуги BDA) и линии AB.
Это означает, что ненулевой вклад в сумму циркуляций по контурам L1 и L2 дают только те части этих контуров, которые вместе составляют первоначальный контур L, тогда как линия, соединяющая точки A и B, проходится дважды – во взаимно противоположных направлениях и, следовательно, соответствующие интегралы в сумме компенсируют друг друга (согласно свойству 1).
Приведенные аргументы сохраняют свою силу и при дальнейшем разбиении контура L на большее число петлей, ибо при суммировании циркуляций по всем образованным контурам интегралы по смежным линиям будут взаимно уничтожаться, так что сумма таких циркуляций сведется к циркуляции по первоначальному контуру. Результаты таких рассуждений можно представить в следующем обобщенном виде.
Следствие. Если область, ограниченную замкнутым контуром L, разбить произвольным образом на n элементов, ограниченных контурами 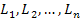 , то циркуляция вектора A по внешнему контуру L равна сумме циркуляций по всем контурам разбиения:
Таким образом, для вычисления циркуляции векторного поля по контуру L можно разбить область, ограниченную контуром, на малые злементы (например, прямоугольники) и просуммировать результаты вычислений циркуляций по границам элементарных областей
|
