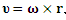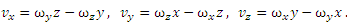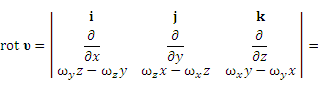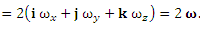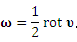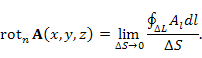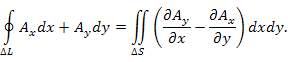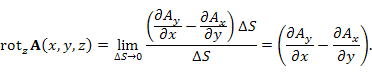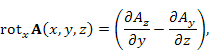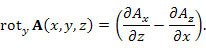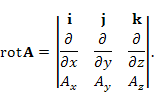Пусть в некоторой окрестности точки 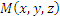 определено векторное поле A. Мысленно проведем через эту точку плоскость, перпендикулярную произвольно выбранному единичному вектору n, и опишем в этой плоскости вокруг точки M замкнутый контур ΔL . Затем составим отношение циркуляции поля A по контуру ΔL к площади ΔS области, ограниченной этим контуром, и перейдем к пределу ΔS → 0, стягивая контур ΔL в точку. Такой предел называется проекцией ротора векторного поля A на направление n и обозначается символическим выражением определено векторное поле A. Мысленно проведем через эту точку плоскость, перпендикулярную произвольно выбранному единичному вектору n, и опишем в этой плоскости вокруг точки M замкнутый контур ΔL . Затем составим отношение циркуляции поля A по контуру ΔL к площади ΔS области, ограниченной этим контуром, и перейдем к пределу ΔS → 0, стягивая контур ΔL в точку. Такой предел называется проекцией ротора векторного поля A на направление n и обозначается символическим выражением
| |
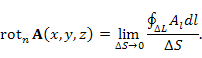
|
(1) |
|
Правило согласования направления обхода контура ΔL с направлением нормали n показано на рисунке 1.
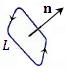 Рис. 1
Рис. 1. Если ручку буравчика вращать по направлению обхода контура, то направление ввинчивания буравчика указывает направление нормали.
 Если нормаль n направить вдоль положительного направления оси z и использовать формулу Грина, то циркуляцию поля A по плоскому контуру ΔL можно представить в виде
Если нормаль n направить вдоль положительного направления оси z и использовать формулу Грина, то циркуляцию поля A по плоскому контуру ΔL можно представить в виде
| |
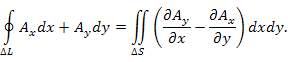 |
(2) |
|
Теорема о среднем позволяет заменить подинтегральную функцию ее значением в некоторой средней точке. Тогда двойной интеграл в правой части последнего равенства принимает вид
Таким образом,
| |
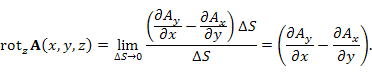 |
(3) |
|
Производя циклическую замену 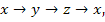 получим выражения для других компонент ротора: получим выражения для других компонент ротора:
| |
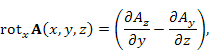 |
(4) |
|
| |
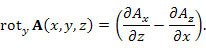 |
(5) |
|
Полученные результаты можно объединить в единую формулу:
| |
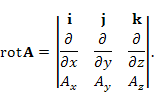 |
(6) |
|
Обоснование формулы (6), не основанное на использовании формулы Грина, содержится в разделе "Вычисление ротора в прямоугольной системе координат"
 Физический смысл ротора векторного поля
Физический смысл ротора векторного поля
 Рассмотрим поток движущеся жидкости. Поместим в некоторую точку этого потока колесико бесконечно малого размера с лопастями, расположенными по его периметру параллельно оси. Под воздействием потока жидкости колесико будет вращаться с некоторой скоростью, величина и направление которой является функцией положения точки. Поле скорости υ вращающегося тела равно векторному произведению
где ω – мгновенная угловая скорость; r – радиус-вектор, проведенный из центра вращения в произвольную точку тела.
Рассмотрим поток движущеся жидкости. Поместим в некоторую точку этого потока колесико бесконечно малого размера с лопастями, расположенными по его периметру параллельно оси. Под воздействием потока жидкости колесико будет вращаться с некоторой скоростью, величина и направление которой является функцией положения точки. Поле скорости υ вращающегося тела равно векторному произведению
где ω – мгновенная угловая скорость; r – радиус-вектор, проведенный из центра вращения в произвольную точку тела.
 Координаты вектора υ равны
Вычислим rot υ:
Координаты вектора υ равны
Вычислим rot υ:
 Таким образом, ротор вектора скорости υ характеризует "вращательную компоненту" поля скоростей:
Таким образом, ротор вектора скорости υ характеризует "вращательную компоненту" поля скоростей:
|
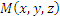 определено векторное поле A. Мысленно проведем через эту точку плоскость, перпендикулярную произвольно выбранному единичному вектору n, и опишем в этой плоскости вокруг точки M замкнутый контур ΔL . Затем составим отношение циркуляции поля A по контуру ΔL к площади ΔS области, ограниченной этим контуром, и перейдем к пределу ΔS → 0, стягивая контур ΔL в точку. Такой предел называется проекцией ротора векторного поля A на направление n и обозначается символическим выражением
определено векторное поле A. Мысленно проведем через эту точку плоскость, перпендикулярную произвольно выбранному единичному вектору n, и опишем в этой плоскости вокруг точки M замкнутый контур ΔL . Затем составим отношение циркуляции поля A по контуру ΔL к площади ΔS области, ограниченной этим контуром, и перейдем к пределу ΔS → 0, стягивая контур ΔL в точку. Такой предел называется проекцией ротора векторного поля A на направление n и обозначается символическим выражением

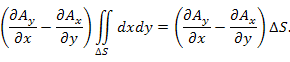
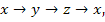 получим выражения для других компонент ротора:
получим выражения для других компонент ротора: