Потенциальные поля имеют большое значение в физических приложениях и обладают важными свойствами.
-
Пусть векторные поля
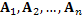 являются потенциальными:
Тогда и результирующее поле
является потенциальным, а его потенциал являются потенциальными:
Тогда и результирующее поле
является потенциальным, а его потенциал 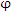 равен сумме потенциалов полей равен сумме потенциалов полей 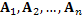 :
Благодаря этому свойству проблема нахождения результирующего векторного поля E сводится к проблеме суммирования скалярных величин с последующим нахождением градиента полученной функции, что существенно сокращает трудоемкость вычислений. :
Благодаря этому свойству проблема нахождения результирующего векторного поля E сводится к проблеме суммирования скалярных величин с последующим нахождением градиента полученной функции, что существенно сокращает трудоемкость вычислений.
-
Пусть скалярное поле
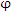 является потенциалом векторного поля A. Тогда криволинейный интеграл является потенциалом векторного поля A. Тогда криволинейный интеграл 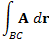 по дуге BC не зависит от пути интегрирования, а определяется только положением начальной и конечной точек по дуге BC не зависит от пути интегрирования, а определяется только положением начальной и конечной точек 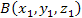 и и 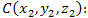 Действительно,
и, следовательно,
Потенциал в произвольной точке
Действительно,
и, следовательно,
Потенциал в произвольной точке 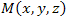 может быть вычислен по формуле
В качестве пути интегрирования проще всего выбрать ломаную, соединяющую точки B и M, участки которой расположены параллельно координатным осям. может быть вычислен по формуле
В качестве пути интегрирования проще всего выбрать ломаную, соединяющую точки B и M, участки которой расположены параллельно координатным осям.
Следствие. Если положения начальной и конечной точек интегрирования совпадают, то интеграл по замкнутому контуру L равен нулю: Если положения начальной и конечной точек интегрирования совпадают, то интеграл по замкнутому контуру L равен нулю:
|