 Пусть задано некоторое потенциальное поле
Пусть задано некоторое потенциальное поле 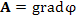 . Рассмотрим две близко расположенные поверхности уровня,
где значения постоянных . Рассмотрим две близко расположенные поверхности уровня,
где значения постоянных 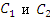 отличаются друг от друга на малую величину. отличаются друг от друга на малую величину.
 При движении вдоль поверхности уровня поле остается постоянным, а чтобы максимально быстро перейти с одной поверхности уровня на другую, нужно двигаться в направлении нормали к поверхности. Это означает, что вектор нормали к поверхности уровня направлен в сторону наиболее быстрого изменения поля
При движении вдоль поверхности уровня поле остается постоянным, а чтобы максимально быстро перейти с одной поверхности уровня на другую, нужно двигаться в направлении нормали к поверхности. Это означает, что вектор нормали к поверхности уровня направлен в сторону наиболее быстрого изменения поля 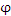 и, следовательно, совпадает по направлению с вектором и, следовательно, совпадает по направлению с вектором 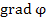 . .
 Подобные интуитивные соображения могут быть положены в основу следующего математического утверждения.
Подобные интуитивные соображения могут быть положены в основу следующего математического утверждения.
Теорема. Векторные линии потенциального поля Векторные линии потенциального поля 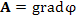 направлены перпендикулярно к поверхностям уровня направлены перпендикулярно к поверхностям уровня 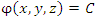
Доказательство. Из уравнения поверхностей уровня Из уравнения поверхностей уровня 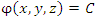 следует равенство нулю дифференциала функции следует равенство нулю дифференциала функции 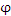 ,
что влечет за собой ортогональность векторов ,
что влечет за собой ортогональность векторов 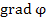 и и 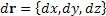 . .
 Поскольку вектор
Поскольку вектор 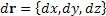 является касательным вектором к поверхности уровня, то вектор является касательным вектором к поверхности уровня, то вектор 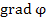 ортогонален этой поверхности. ортогонален этой поверхности.
 Рисунок 1 иллюстрирует ортогональность векторных линий потенциального поля и поверхностей уровня.
Рисунок 1 иллюстрирует ортогональность векторных линий потенциального поля и поверхностей уровня.
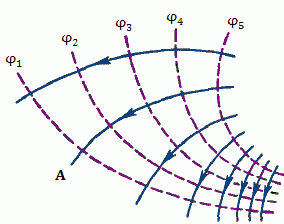
 Рис. 1
Рис. 1. Векторные линии поля 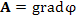 (сплошные линии со стрелками) перпендикулярны к эквипотенциальным поверхностям скалярного поля 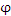 .
|
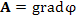 . Рассмотрим две близко расположенные поверхности уровня,
. Рассмотрим две близко расположенные поверхности уровня,
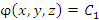 и
и 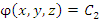 ,
,
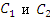 отличаются друг от друга на малую величину.
отличаются друг от друга на малую величину.
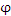 и, следовательно, совпадает по направлению с вектором
и, следовательно, совпадает по направлению с вектором 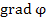 .
.
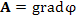 направлены перпендикулярно к поверхностям уровня
направлены перпендикулярно к поверхностям уровня 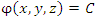
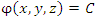 следует равенство нулю дифференциала функции
следует равенство нулю дифференциала функции 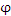 ,
,
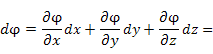
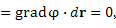
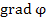 и
и 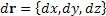 .
.
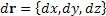 является касательным вектором к поверхности уровня, то вектор
является касательным вектором к поверхности уровня, то вектор 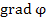 ортогонален этой поверхности.
ортогонален этой поверхности.

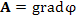 (сплошные линии со стрелками) перпендикулярны к эквипотенциальным поверхностям скалярного поля
(сплошные линии со стрелками) перпендикулярны к эквипотенциальным поверхностям скалярного поля 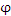 .
.