-
Поток тепла в теле с температурным распределением T(x, y, z) описывается уравнением распространения тепла
где K > 0 – коэффициент теплопроводности, являющийся характеристикой вещества.
Таким образом,
и, следовательно, векторное поле h является потенциальным.
Наличие знака минус отражает физику протекающего процесса, поскольку градиент температуры направлен в сторону наиболее быстрого возрастания температуры, тогда как тепловой поток распространяется в противоположном направлении, из нагретой области – в охлажденную.
-
Закон всемирного тяготения устанавливает, что любые тела притягиваются друг к другу с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между центрами масс:
Введем гравитационный потенциал
Тогда силу гравитационного притяжения тела единичной массы m = 1 можно представить в виде градиента скалярного поля
 :
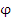Это означает, что векторное поле сил гравитационного взаимодействия является потенциальным полем и, следовательно, работа сил этого поля не зависит от пути перемещения тела из одной точки в другую.
-
Напряженность электрического поля
|
Напряженностью электрического поля
называеся сила, действующая со стороны поля на единичный положительный заряд.
Ссылаясь на векторное электрическое поле, обычно подразумевают напряженность этого поля.
|
E , образованного точечным зарядом q, описывается векторным равенством
и, следовательно, связана с потенциалом
соотношением
 .
Отрицательный знак перед grad φ означает, что сила, действующая на положительно заряженную частицу со стороны электрического поля, направлена в сторону наиболее быстрого убывания скалярного поля.
Таким образом, электрическое поле является потенциальным. Работа сил электрического поля не зависит от пути перемещения заряженной частицы из одной точки в другую и равна разности потенциалов между этими точками.
|
