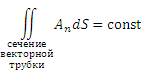Конев В.В.  Скалярные и векторные поля

| Словарь | Калькулятор | Тесты | Задачи и упражнения |
| Скалярные и векторные поля. Градиент | Ротор. Типы полей. Системы координат |
Соленоидальное поле
      Векторное поле  A  называется соленоидальным, если дивергенция этого поля равна нулю:  div A = 0. В таком поле - согласно теореме Остроградского-Гаусса - поток вектора  A  через любую замкнутую поверхность равен нулю:
Другими словами, в отсутствии источников поля поток вовнутрь некоторой области равен с противоположным знаком потоку из этой области наружу. Сумма таких потоков равна нулю.
     Для примера рассмотрим поток соленоидального поля через внешнюю поверхность векторной трубки между двумя произвольными сечениями  S1  и  S2 .

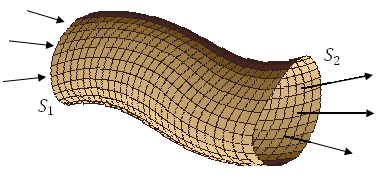Рис. 1. Векторная трубка между двумя сечениями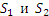
Образующими векторной трубки являются векторные линии поля  A. Поэтому проекция вектора  A  на нормаль к поверхности трубки равна нулю, что означает равенство нулю потока поля  A  через ее поверхность. Тогда равна нулю и сумма потоков поля  A  наружу через сечения :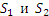
.
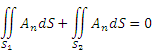Если в сечении  S1  изменить направление нормали так, чтобы оно было согласовано с направление нормали в сечении  S2  (как это показано на рисунке 1), то получим следующее важное свойство соленоидального поля.
Поток соленоидального поля через любое поперечное сечение векторной трубки сохраняет постоянное значение:
Этому свойству можно дать следующую гидродинамическую интерпретацию: в случае несжимаемой жидкости и в отсутствии источников поля расход жидкости через любое поперечное сечение имеет одно и то же значение.
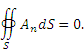
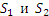
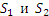
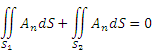
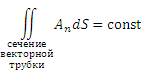
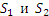
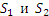
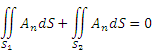