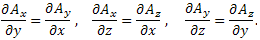Векторное поле A назывется потенциальным, если его можно представить в виде градиента некоторого скалярного поля 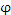 :
Само скалярное поле :
Само скалярное поле 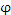 называется при этом потенциалом векторного поля A. называется при этом потенциалом векторного поля A.
 Иначе говоря, векторное поле A является потенциальным, если координаты вектора A можно представить в виде частных производных некоторого скаляного поля
Иначе говоря, векторное поле A является потенциальным, если координаты вектора A можно представить в виде частных производных некоторого скаляного поля 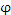 :
Условия потенциальности поля. :
Условия потенциальности поля.
 Пусть
Пусть 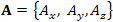 – дифференцируемое потенциальное поле, – дифференцируемое потенциальное поле, 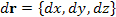 – бесконечно малый вектор смещения их произвольной точки – бесконечно малый вектор смещения их произвольной точки 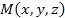 . .
 Рассмотрим скалярное произведение векторов A и dr:
Выражение в правой части этого равенства представляет собой полный дифференциал функции
Рассмотрим скалярное произведение векторов A и dr:
Выражение в правой части этого равенства представляет собой полный дифференциал функции 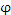 . Если частные производные . Если частные производные 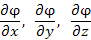 являются непрерывными функциями, то смешанные производные от являются непрерывными функциями, то смешанные производные от 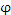 не зависят от порядка дифференцирования:
Учитывая, что частные производные от функции не зависят от порядка дифференцирования:
Учитывая, что частные производные от функции 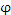 являются координатами вектора A, получаем следующие условия потенциальности поля A: являются координатами вектора A, получаем следующие условия потенциальности поля A:
|
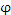 :
:
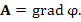
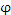 называется при этом потенциалом векторного поля A.
называется при этом потенциалом векторного поля A.
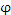 :
:
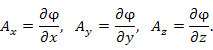
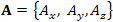 – дифференцируемое потенциальное поле,
– дифференцируемое потенциальное поле, 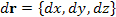 – бесконечно малый вектор смещения их произвольной точки
– бесконечно малый вектор смещения их произвольной точки 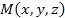 .
.
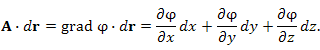
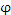 . Если частные производные
. Если частные производные 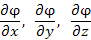 являются непрерывными функциями, то смешанные производные от
являются непрерывными функциями, то смешанные производные от 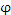 не зависят от порядка дифференцирования:
не зависят от порядка дифференцирования:
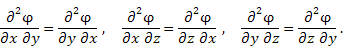
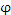 являются координатами вектора A, получаем следующие условия потенциальности поля A:
являются координатами вектора A, получаем следующие условия потенциальности поля A: