Рассмотрим физический смысл потока векторного поля на примере гидродинамической задачи о вычислении количества жидкости, протекающей через поверхность S в единицу времени.
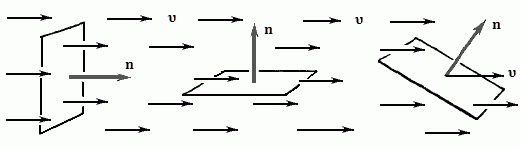
 Каждой точке заполненного жидкостью пространства можно поставить в соответствие вектор скорости υ частиц потока текущей жидкости.
Каждой точке заполненного жидкостью пространства можно поставить в соответствие вектор скорости υ частиц потока текущей жидкости.
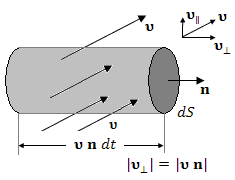
 Разложим вектор υ скорости движения жидкости вблизи площадки на две составляющие, одна из которых направлена вдоль поверхности dS, а другая – перпендикулярно к ней. За протекание жидкости через площадку ответственна только нормальная составляющая скорости υn = υ · n, где n – единичный вектор нормали к поверхности dS.
Разложим вектор υ скорости движения жидкости вблизи площадки на две составляющие, одна из которых направлена вдоль поверхности dS, а другая – перпендикулярно к ней. За протекание жидкости через площадку ответственна только нормальная составляющая скорости υn = υ · n, где n – единичный вектор нормали к поверхности dS.
 За время dt через площадку пройдет жидкость, отстоящая от нее на расстоянии υn dt и заполняющая объем υn dt dS .
За время dt через площадку пройдет жидкость, отстоящая от нее на расстоянии υn dt и заполняющая объем υn dt dS .
 Объем жидкости, протекающей через бесконечно малую проницаемую площадку dS за время dt, равен (с точностью до знака)
Объем жидкости, протекающей через бесконечно малую проницаемую площадку dS за время dt, равен (с точностью до знака)
 В единицу времени через поверхность dS проходит
В единицу времени через поверхность dS проходит 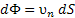 единиц объема жидкости. Эта величина называется потоком вектора υ через элемент поверхности dS . единиц объема жидкости. Эта величина называется потоком вектора υ через элемент поверхности dS .
 Для нахождения потока Φ вектора υ через поверхность конечных размеров нужно разбить эту поверхность на малые элементы и просуммировать потоки через все элементы. Результатом такого суммирования является интегральная сумма, которая переходит в соответствующий поверхностный интеграл при замене элементов конечных размеров бесконечно малыми элементами разбиения поверхности.
Для нахождения потока Φ вектора υ через поверхность конечных размеров нужно разбить эту поверхность на малые элементы и просуммировать потоки через все элементы. Результатом такого суммирования является интегральная сумма, которая переходит в соответствующий поверхностный интеграл при замене элементов конечных размеров бесконечно малыми элементами разбиения поверхности.
 Таким образом, количество жидкости, протекающей через S в единицу времени равно потоку вектора υ через поверхность S, то есть поверхностному интегралу от проекции вектора υ на нормаль к поверхности:
Таким образом, количество жидкости, протекающей через S в единицу времени равно потоку вектора υ через поверхность S, то есть поверхностному интегралу от проекции вектора υ на нормаль к поверхности:
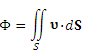 .
|
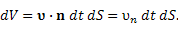
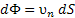 единиц объема жидкости. Эта величина называется потоком вектора υ через элемент поверхности dS .
единиц объема жидкости. Эта величина называется потоком вектора υ через элемент поверхности dS .
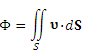 .
.