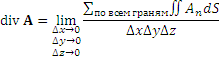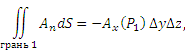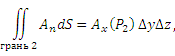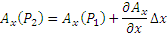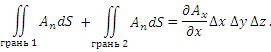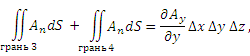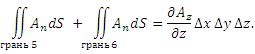Теорема. Если векторное поле A - дифференцируемая функция, то в прямоугольной системе координат дивергенцию этого поля можно представить в виде
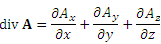 ,
где Ax, Ay и Az – координаты вектора A .
Доказательство. По определению, div A в точке M(x, y, z) равна пределу отношения потока векторного поля через замкнутую поверхность ΔS , окружающую эту точку, к объему Δ V области, заключенной внутри поверхности, при ΔV → 0. По определению, div A в точке M(x, y, z) равна пределу отношения потока векторного поля через замкнутую поверхность ΔS , окружающую эту точку, к объему Δ V области, заключенной внутри поверхности, при ΔV → 0.
 Рассмотрим поток вектора A через внешнюю поверхность бесконечно малого параллелепипеда, ребра которого равны Δx , Δy и Δz, а грани расположены параллельны координатным плоскостям некоторой прямоугольной системы координат.
Рассмотрим поток вектора A через внешнюю поверхность бесконечно малого параллелепипеда, ребра которого равны Δx , Δy и Δz, а грани расположены параллельны координатным плоскостям некоторой прямоугольной системы координат.
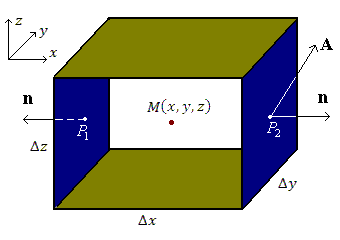 Рис. 1
Рис. 1. Рис. 1. Поток вектора A через внешнюю поверхность параллелепипеда.
 Представим этот поток в виде суммы потоков через все грани параллелепипеда. Учитывая, что ΔV = Δx Δy Δz , запишем выражение для дивергенции поля в виде
(Напомним, что An – проекция вектора A на направление внешней нормали.)
Представим этот поток в виде суммы потоков через все грани параллелепипеда. Учитывая, что ΔV = Δx Δy Δz , запишем выражение для дивергенции поля в виде
(Напомним, что An – проекция вектора A на направление внешней нормали.)
 Найдем поток вектора A через две противоположные грани, окрашенные на рисунке 1 синим цветом. Внешняя нормаль к правой грани совпадает с положительным направлением оси 0x и, следовательно, An = Ax .
Найдем поток вектора A через две противоположные грани, окрашенные на рисунке 1 синим цветом. Внешняя нормаль к правой грани совпадает с положительным направлением оси 0x и, следовательно, An = Ax .
 Внешняя нормаль к левой грани направлена в противоположную сторону и, таким образом, на этой грани An = –Ax. В виду малости граней параллелепипеда, функции Ax можно заменить их значениями в центрах соответствующих граней. Тогда
где P1 и P2 – точки в центрах граней.
Внешняя нормаль к левой грани направлена в противоположную сторону и, таким образом, на этой грани An = –Ax. В виду малости граней параллелепипеда, функции Ax можно заменить их значениями в центрах соответствующих граней. Тогда
где P1 и P2 – точки в центрах граней.
 Значения функции Ax в точках P1 и P2 , расположенных на малом расстоянии Δx друг от друга, связаны между собой соотношением
Тогда сумма потоков через грани 1 и 2 равна
Аналогичные результаты получаются для суммарных потоков через другие пары противоположных граней:
Подстановка полученных выражений в соответствующую формулу для дивергенции поля A завершает доказательство.
Значения функции Ax в точках P1 и P2 , расположенных на малом расстоянии Δx друг от друга, связаны между собой соотношением
Тогда сумма потоков через грани 1 и 2 равна
Аналогичные результаты получаются для суммарных потоков через другие пары противоположных граней:
Подстановка полученных выражений в соответствующую формулу для дивергенции поля A завершает доказательство.
|
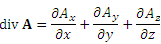 ,
,

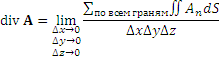
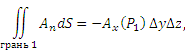
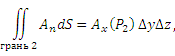
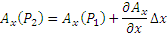
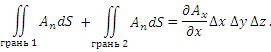
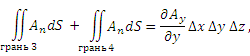
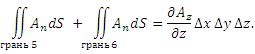
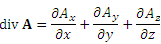 ,
,