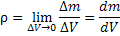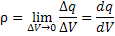Рассмотрим произвольную точку M (x, , y, z) и опишем вокруг этой точки замкнутую поверхность ΔS.
 Составим отношение потока
Составим отношение потока 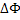 вектора A через поверхность ΔS к объему ΔV области, ограниченной этой поверхностью. Затем перейдем к пределу ΔV → 0, стягивая поверхность ΔS в точку. вектора A через поверхность ΔS к объему ΔV области, ограниченной этой поверхностью. Затем перейдем к пределу ΔV → 0, стягивая поверхность ΔS в точку.
 Полученный предел называется дивергенцией векторного поля A и обозначается символическим выражением div A .
Полученный предел называется дивергенцией векторного поля A и обозначается символическим выражением div A .
 Таким образом,
Таким образом,
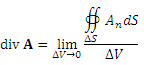 .
 Определение дивергенции векторного поля A можно также представить в виде
Если сопоставить определение дивергенции с определениями
плотности распределения массы
Определение дивергенции векторного поля A можно также представить в виде
Если сопоставить определение дивергенции с определениями
плотности распределения массы
Плотность распределения массы m
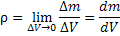
|
или плотности распределения заряда,
Плотность распределения заряда q
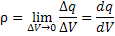
|
то можно сказать, что дивергенция векторного поля A представляет собой плотность распределения потока векторного поля A.
 Суть понятия "дивергенция векторного поля" выявляется особенно наглядно, если обратиться к уравнению Максвелла
Суть понятия "дивергенция векторного поля" выявляется особенно наглядно, если обратиться к уравнению Максвелла
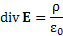 ,
которое в явном виде связывает дивергенцию электрического поля E с плотностью ρ распределения зарядов – источников электрического поля. Иначе говоря, дивергенция векторного поля представляет собой плотность распределения источников поля.
|
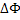 вектора A через поверхность ΔS к объему ΔV области, ограниченной этой поверхностью. Затем перейдем к пределу ΔV → 0, стягивая поверхность ΔS в точку.
вектора A через поверхность ΔS к объему ΔV области, ограниченной этой поверхностью. Затем перейдем к пределу ΔV → 0, стягивая поверхность ΔS в точку.
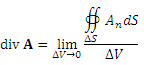 .
.
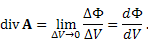
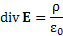 ,
,