Рассмотрим поток векторного поля A черех поверхность S в направлении внешней нормали n к поверхности.
-
Пусть символы S + и S – обозначают две стороны поверхности S. Тогда при переходе с одной стороны поверхности на другую напраление вектора нормали изменяется на противоположное и, соответственно, проекция вектора A на нормаль изменяет свой знак. Следовательно,
-
Пусть S представляет собой замкнутую поверхность, ограничивающую область V. Разделим эту область перегородкой D на две части,
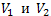 . Обозначим поверхности, ограничивающие области . Обозначим поверхности, ограничивающие области 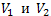 , символами , символами 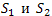 соответственно. соответственно.
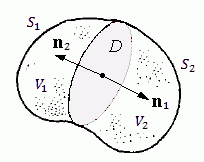 Рис. 1
Рис. 1. Замкнутая поверхность S является границей области V. Поверхности 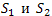 включают в себя внешние стороны перегородки D (с направлениями нормали наружу).
Тогда поток векторного поля A через поверхность S равен сумме потоков через поверхности поток векторного поля A через поверхность S равен сумме потоков через поверхности 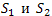 : :
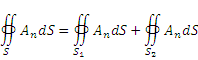 .
Действительно, каждая из поверхностей 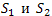 включает в себя в качестве составной части перегородку D, вклады которой в потоки включает в себя в качестве составной части перегородку D, вклады которой в потоки 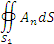 и и 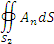 равны по абсолютной величине, но имеют противоположные знаки, поскольку нормаль к перегородке D изменяет свое напрвление на противоположное при переходе с одной стороны поверхности D на другую. Оставшиеся части поверхностей равны по абсолютной величине, но имеют противоположные знаки, поскольку нормаль к перегородке D изменяет свое напрвление на противоположное при переходе с одной стороны поверхности D на другую. Оставшиеся части поверхностей 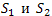 вместе составляют поверхность S. вместе составляют поверхность S.
Следствие. Если область V разделить произвольным образом на k элементов Если область V разделить произвольным образом на k элементов 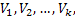 ограниченных поверхностями ограниченных поверхностями 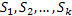 , то поток вектора A через внешнюю поверхность S равен сумме потоков через замкнутые поверхности , то поток вектора A через внешнюю поверхность S равен сумме потоков через замкнутые поверхности 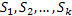 : :
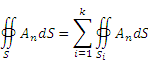 .
Для доказательства этого утверждения достаточно разбить область V на две части, затем произвести разбиение полученных областей и так далее.
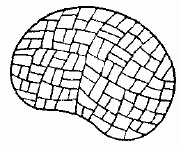 Рис. 2
Рис. 2. Разбиение области V на элементарные области.
|