Дивергенция векторного поля A в точке 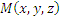 определяется формулой определяется формулой
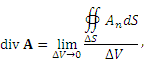
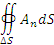 – поток вектора A через замкнутую поверхность ΔS, описанную вокруг точки M ; ΔV – объем области, ограниченной этой поверхностью. – поток вектора A через замкнутую поверхность ΔS, описанную вокруг точки M ; ΔV – объем области, ограниченной этой поверхностью.
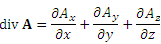 , ,
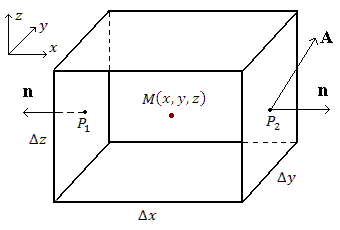
Рис. 1. Точка M находится в центре малого параллелепипеда, грани которого расположены параллельно координатным плоскостям прямоугольной системы координат. За направление нормали к каждой грани выбирается направление наружу. 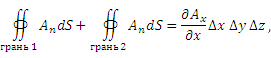
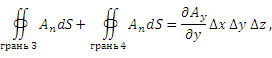
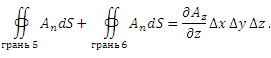
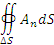 через замкнутую поверхность ΔS. через замкнутую поверхность ΔS.
Остается только подставить полученные результаты в выражение для дивергенции. Представление дивергенции с помощью оператора набла. 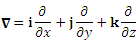 и векторной функции и векторной функции 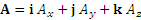 : :
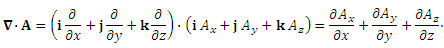
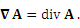
|