Конев В.В.   Несобственные интегралы

| Разделы курса | Примеры | Калькулятор |      
 
| Пределы | Дифференцирование | Неопределенные интегралы | Определенные интегралы |
Интегралы от неограниченных функций
        Точка  x = a  называется особой точкой функции  f(x), если  f(x) → ∞  при  x → a.

      Пусть точка  x = a  является особой точкой функции  f(x)  и при этом функция  f(x)  интегрируема на любом конечном промежутке  [c, b], где  a < c < b. Тогда конечный или бесконечный предел интеграла 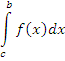   при  c → a + 0  называется несобственным интегралом функции  f(x)  на промежутке  [a, b]:
   (1)  
      Если этот предел существует и конечен, то говорят, что несобственный интеграл (1) сходится. В противном случае интеграл (1) называют расходящимся.
      В случае, когда особая точка функции  f(x)  совпадает с верхним пределом интегрирования, несобственный интеграл 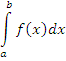   определяется уравнением
   (2)  
      Определения (1) и (2) можно представить единой формулой
   (3)  
подразумевая под  F(b)  и  F(a)  предельные значения первообразной  F(x)  функции  f(x)  при  x → b  и  x → a  соответственно.

      Если особая точка  c  функции  f(x)  является внутренней точкой промежутка  [a, b], то
  .  (4)  

      Интеграл от функции, неограниченной в окрестности точки  a  (или  b), геометрически можно интерпретировать как площадь области, заключенной между кривой  y = f(x)  и осью ординат. При этом единственно существенным обстоятельством, определяющим сходимость интеграла 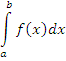 , является поведение функции  f(x)  в достаточно малой окрестности особой точки, а именно быстрота приближения кривой  y = f(x)  к оси  0y  при  x → a  (или при  x → b, если точка  b  является точкой разрыва).


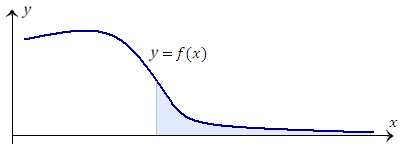
Рис. 1. Поведение функции  f(x)  при не очень больших значениях  x  является несущественным для сходимости интеграла 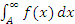, а определяющее значение имеет лишь быстрота приближения кривой  y = f(x)  к оси  0x  при  x→ ∞.
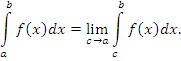
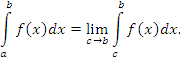
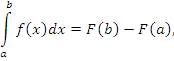
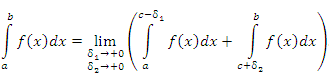