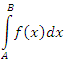Несобственные интегралы первого рода

Несобственные интегралы

Основные понятия Несобственные интегралы первого рода Признаки сравнения Эталонные p-интегралы первого рода Признаки сходимости Абеля и Дирихле Абсолютная и условная сходимости Интегралы от неограниченных функций Признаки сравнения интегралов от неограниченных функций P–интегралы от неограниченных функций Некоторые приемы исследования интегралов на сходимость Интеграл Эйлера и связанные с ним интегралы Вычисление несобственных интегралов Главное значение интеграла Интегралы первого рода в смысле главного значения Обобщенные значения интегралов

Пусть функция f(x) определена для

и при этом интеграл

(1)

имеет смысл для любых значений B > A.
Тогда под несобственным интегралом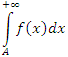

понимается предельное значение (конечное или нет) определенного интеграла (1) при B → +∞ :

(2)

Аналогичным образом определяется интегралы вида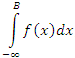

		(3)
		(4)

Несобственный и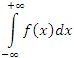нтеграл называется сходящимся, если существует конечный предел соответствующего определенного интеграла. В противном случае говорят, что несобственный интеграл расходится.

Используя формулу Ньютона-Лейбница, определение (2) несобственного интеграла с бесконечным верхним пределом может быть представлено в виде

(5)

где F(x) - первообразная функции f(x);

Аналогично,

		(6)
		(7)

Например,

(8)

Конев В.В. Несобственные интегралы