|
В основе признаков сравнения лежат вполне очевидные соображения. Например, если
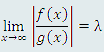 , где λ – конечное число, то (начиная с некоторого достаточно большого значения x) выполняется приближенное равенство f(x) ≈ λg(x). Тогда и площади областей, расположенных между соответствующими кривыми и осью абсцисс, отличаются друг от друга в конечное число раз. Если одна из них конечна, то конечна и другая. , где λ – конечное число, то (начиная с некоторого достаточно большого значения x) выполняется приближенное равенство f(x) ≈ λg(x). Тогда и площади областей, расположенных между соответствующими кривыми и осью абсцисс, отличаются друг от друга в конечное число раз. Если одна из них конечна, то конечна и другая.
 . .
|
|
|
Метод исследования несобственного интеграла на сходимость, основанный на вычислении предела первообразной функции, далеко не всегда может рассматриваться как наиболее оптимальный. На практике обычно прибегают к признакам сравнения или признакам сходимости. Суть типичного признака сравнения заключается в следующем.
Признак сравнения 1. Пусть функции f(x) и g(x) определены на промежутке (A,B) и удовлетворяют неравенству 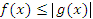 , где A и B – любые числа (не обязательно конечные). Тогда , где A и B – любые числа (не обязательно конечные). Тогда
1) из сходимости интеграла  вытекает сходимость интеграла вытекает сходимость интеграла 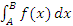 . .
2) расходимость интеграла 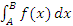 влечет расходимость интеграла влечет расходимость интеграла  . .
Другими словами, исследуемый на сходимость интеграл сравнивается с эталонным. Если эталонный интеграл больше исследуемого и сходится, то сходится и исследуемый. Если же эталонный интеграл меньше исследуемого и расходится, то расходится и исследуемый. Если существует отличный от нуля предел функции f(x) при 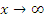 , то интеграл , то интеграл 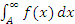 расходится. Однако равенство нулю такого предела не является достаточным условием сходимости этого интеграла. Например, расходится. Однако равенство нулю такого предела не является достаточным условием сходимости этого интеграла. Например, 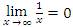 , тогда как интеграл , тогда как интеграл 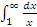 расходится. расходится.
Признак сравнения 1 можно переформулировать, положив в основу сопоставление быстроты изменения исследуемой и эталонной функций в окрестности соответствующей точки "несобственности" (в том числе и бесконечно удаленной). Признак сравнения 2. Если существует предел 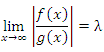 , то , то
при 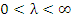 интегралы интегралы 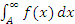 и и 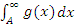 сходятся или расходятся одновременно; сходятся или расходятся одновременно;
при 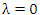 сходимость интеграла сходимость интеграла 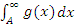 влечет за собой сходимость интеграла влечет за собой сходимость интеграла 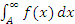 ; ;
при 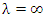 из расходимости интеграла из расходимости интеграла 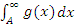 вытекает расходимость интеграла вытекает расходимость интеграла 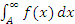 . .
Аналогичным образом формулируются признаки сходимости интегралов вида 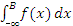 . .
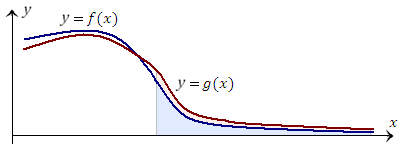
С геометрической точки зрения сходимость интеграла 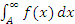 означает, что площадь области, заключенной между кривой y = f(x) и осью абсцисс, конечна. означает, что площадь области, заключенной между кривой y = f(x) и осью абсцисс, конечна.
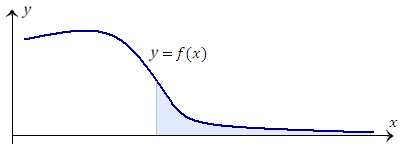
Рис. 1. Определяющее значение для сходимости или расходимости интеграла 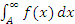 имеет лишь быстрота приближения кривой y = f(x) к оси 0x при x→ ∞. имеет лишь быстрота приближения кривой y = f(x) к оси 0x при x→ ∞.
|