| |
-
Доказать сходимость интеграла Эйлера
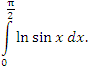
Интегрируя по частям, получаем
| |
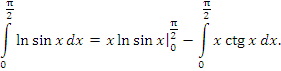
|
(1) |
|
Учитывая предельное соотношение
заключаем, что интеграл в правой части уравнения (1) является собственным, а первый член равен нулю:
Таким образом, рассматриваемый интеграл допускает представление в виде собственного интеграла
| |
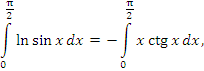
|
(2) |
|
что доказывет его сходимость. (Другое обоснование сходимости интеграла Эйлера см. в разделе "Интеграл Эйлера".)
-
Чтобы доказать сходимость интеграла
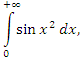 выполним подстановку выполним подстановку 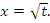 Тогда Тогда
| |
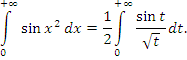
|
(3) |
|
Полученный интеграл сходится (см. Пример 1).
-
Аналогично устанавливается сходимость интеграла
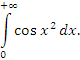
Действительно, представим этот интеграл в виде
| |
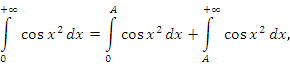
|
(4) |
|
где A - конечное положительное число.
Первый член в правой части этого равенства представляет собой собственный интеграл. Преобразуем второе слагаемое, выполнив подстановку 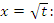
| |
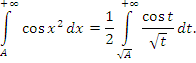
|
(5) |
|
Полученный интеграл сходится (см. Пример 2).
Теорема. Пусть периодическая функция f(x) с периодом T определена на промежутке [A, +∞) и не имеет особых точек на промежутке [A, A + T], а функция g(x) монотонно стремится к нулю при x → +∞. Тогда выполение условия
| |
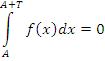
|
(6) |
|
влечет за собой сходимость несобственного интеграла 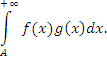
Доказательство. Функция g(x) удовлетворяет условию Дирихле. Поэтому достаточно убедиться в выполнении другого условия, а именно в ограниченности интеграла
| |
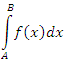
|
(7) |
|
при любом B > A.
Пусть промежуток [A, B] содержит n промежутоков длиной T (n = 0, 1, 2, ...) и некоторый остаточный промежуток [C, B] , длина которого меньше T. Согласно теореме о периодических функциях интеграл 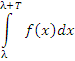 по промежутку, длина которого равна периоду функции f(x), не зависит от λ. Тогда по промежутку, длина которого равна периоду функции f(x), не зависит от λ. Тогда
| |
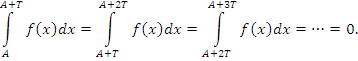
|
(8) |
|
Разбивая промежуток [A, B] вышеуказанным образом и учитывая равенства (8), получаем следующее представление интеграла (7):
| |
 . .
|
(9) |
|
Интеграл в правой части этого равенства является собственным, что доказывает ограниченность интеграла (7) при любом B > A.
|
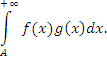
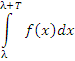 по промежутку, длина которого равна периоду функции f(x), не зависит от λ. Тогда
по промежутку, длина которого равна периоду функции f(x), не зависит от λ. Тогда
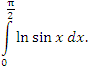
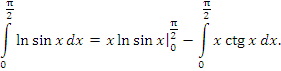
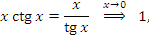
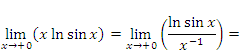
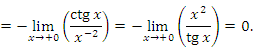
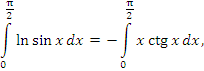
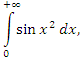 выполним подстановку
выполним подстановку 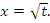 Тогда
Тогда
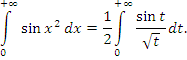
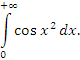
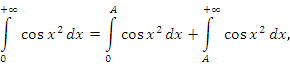
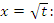
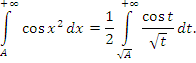
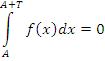
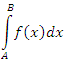
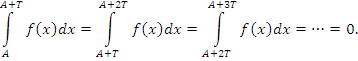
 .
.