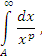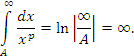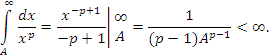При исследования несобственных интегралов вида 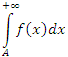 на сходимость с помощью признаков сравнения используются различные эталонные интегралы, важную роль среди которых играют p-интегралы на сходимость с помощью признаков сравнения используются различные эталонные интегралы, важную роль среди которых играют p-интегралы
Область значений параметра p, в которой p-интеграл (1) сходятся, легко устанавливается непосредственным интегрированием.
Проблема исследования на сходимость несобственных интегралов вида 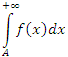 легко разрешается, если при x → ∞ функция f(x) является бесконечно малой порядка p по сравнению с легко разрешается, если при x → ∞ функция f(x) является бесконечно малой порядка p по сравнению с  . Тогда при p > 1 интеграл от f(x) сходится, а при p ≤ 1 - расходится. . Тогда при p > 1 интеграл от f(x) сходится, а при p ≤ 1 - расходится.
Например, функция 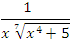
 и, следовательно, интеграл и, следовательно, интеграл  сходится. сходится.
Аналогично, интеграл 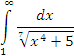 расходится, поскольку функция расходится, поскольку функция 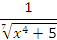 является бесконечно малой порядка 4/7 по сравнению с является бесконечно малой порядка 4/7 по сравнению с  (при x → ∞). (при x → ∞).
|