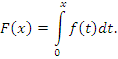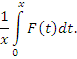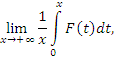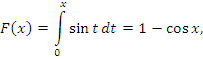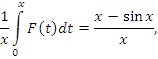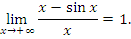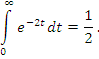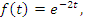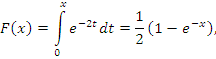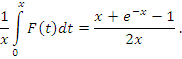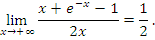|
Здесь мы рассмотрим метод, позволяющий приписывать некоторым расходящимся интегралам обобщенные значения.
Пусть функция f(x) интегрируема на промежутке [0,x] и пусть
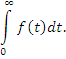
Найдем, например, обобщенное значение расходящегося интеграла 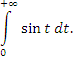 Очевидно, что Очевидно, что
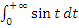 равно 1. равно 1.
Можно показать, что обобщенное значение сходящегося интеграла 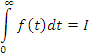 совпадает со значением I этого интеграла (см., например, Фихтенгольц). Для примера обратимся к интегралу
совпадает со значением I этого интеграла (см., например, Фихтенгольц). Для примера обратимся к интегралу
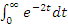 равно равно
|