Признак сходимости Дирихле. Пусть при B > A функция f(x) интегрируема на промежутке [A,B] и пусть функция g(x) монотонно стремится к нулю при x → +∞. Если первообразная
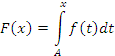
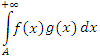 сходится. сходится.
Опуская доказательство признака сходимости Дирихле, обсудим простой поучительный пример. Рассмотрим интеграл 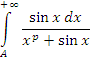 . .
Пусть 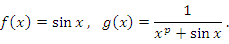
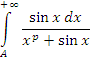 для p ≥ 1 и оставляет вопрос открытым для 0 < p < 1. Более детальное исследование показывает, что рассматриваемый интеграл сходится при p > 1/2 и расходится при других значениях p (см. Пример 5). Отсутствие монотонности стремления к нулю функции решительно изменяет ситуацию со сходимосью интеграла. для p ≥ 1 и оставляет вопрос открытым для 0 < p < 1. Более детальное исследование показывает, что рассматриваемый интеграл сходится при p > 1/2 и расходится при других значениях p (см. Пример 5). Отсутствие монотонности стремления к нулю функции решительно изменяет ситуацию со сходимосью интеграла.
Признак сходимости Абеля. Пусть интеграл 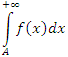 сходится. Если функция g(x) монотонна и ограничена сверху на промежутке [A, ∞), то интеграл сходится. Если функция g(x) монотонна и ограничена сверху на промежутке [A, ∞), то интеграл 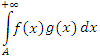 сходится. сходится.
Заметим, что признак сходимости Абеля является следствием признака сходимости Дирихле. Действительно, пусть функции f(x) и g(x) удовлетворяют условиям Абеля. Тогда для монотонной и ограниченной сверху функции g(x) существует конечный предел 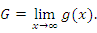
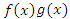 в виде суммы в виде суммы
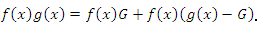
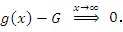 . .
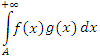 сходится. сходится.
|