Конев В.В.   Несобственные интегралы

| Разделы курса | Примеры | Калькулятор |      
 
| Пределы | Дифференцирование | Неопределенные интегралы | Определенные интегралы |
Абсолютная и условная сходимости
        В некоторых приложениях несобственных интегралов возникает необходимость использования углубленного понятия сходимости. (Одно из таких приложений рассматривается в разделе "Интегралы, зависящие от параметра".) С этой целью рассмотрим следующие возможные случаи.
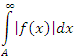  1. Пусть функция  f(x)  интегрируема на полубесконечном интервале  [A, ∞). Если наряду с интегралом    сходится и интеграл  , то интеграл    называется абсолютно сходящимся. Говорят также, что функция  f(x)  абсолютно интегрируема на промежутке  [A, ∞).
  2. Если интеграл    сходится, тогда как интеграл    расходится, то интеграл    называется условно сходящимся.
      Заметим, что из сходимости интеграла    вытекает сходимость интеграла 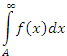 , тогда как обратное утверждение является несправедливым.

      Приведем полезные свойства абсолютно интегрируемых функций, доказательство которого предоставляется читателю.

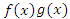  • Пусть функция  f(x)  абсолютно интегрируема на промежутке  [A, ∞). Если функция  g(x)  ограничена на этом промежутке, то и произведение является абсолютно интегрируемой функцией на промежутке  [A, ∞).

  • Если функция  f(x)  абсолютно интегрируема на промежутке  [A, ∞)  и  | g(x) | ≤ | f(x) |, то и функция  g(x)  абсолютно интегрируема на промежутке  [A, ∞).