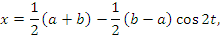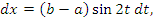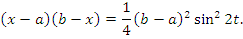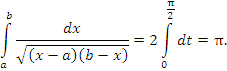|
Вычисление несобственных интегралов сводится к применению стандартных методов интегрирования. Только при этом добавляются два новых элемента:
1) исследование интегралов на сходимость; 2) выполнение предельных переходов. Кроме того, если несобственный интеграл 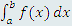 содержит несколько особых точек (точек "несобственности"), то его необходимо разбить на соответствующее число интегралов: содержит несколько особых точек (точек "несобственности"), то его необходимо разбить на соответствующее число интегралов:

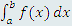 сходится в том и только в том случае, если сходится каждый из интегралов в правой части равенства (1). сходится в том и только в том случае, если сходится каждый из интегралов в правой части равенства (1).
|
|||||||||||||||||||||
|
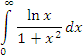 . Представим его в виде суммы двух несобственных интегралов:
. Представим его в виде суммы двух несобственных интегралов:
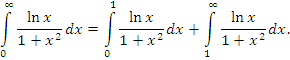
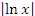 с соответствующим поведением функции
с соответствующим поведением функции 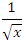 при x → 0, вычислив предел отношения этих функций:
при x → 0, вычислив предел отношения этих функций:
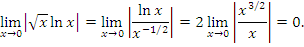
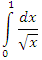 сходится, то сходится и интеграл
сходится, то сходится и интеграл 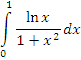 .
.
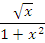 . Учитывая выполнение неравенства
. Учитывая выполнение неравенства 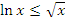 при x → ∞, заключаем, что интеграл
при x → ∞, заключаем, что интеграл 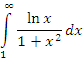 сходится.
сходится.
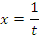 :
:
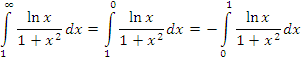 .
.
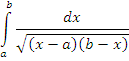 применим подстановку
применим подстановку
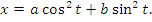 .
.