| |
При исследования на сходимость интегралов от функций, неограниченных на промежутке интегрирования, в качестве эталонных интегралов используются p-интегралы вида
| |
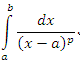
|
(1) |
|
| |
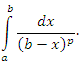
|
(2) |
|
Очевидно, что интегралы (1) и (2) расходятся, если p = 1. Тогда эти интегралы расходятся и при p > 1, поскольку с увеличением p подынтегральные функции возрастают в окрестности особых точек x = a или x = b соответственно.
Если p < 1, то интегралы (1) и (2) сходятся, например,
| |
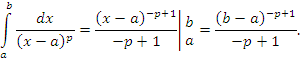
|
(3) |
|
Таким образом, p-интегралы (1) и (2) сходятся при p < 1; расходятся при p ≥ 1.
Используя признак сравнения 2 и выбирая p-интерграл (1) или (2) в качестве эталонного интерграла, можно сформулировать следующие критерии.
-
Если при x → a функция f(x) является бесконечно большой порядка p по сравнению с
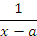 , то интерграл (1) при p < 1 сходится, а при p ≥ 1 - расходится. , то интерграл (1) при p < 1 сходится, а при p ≥ 1 - расходится.
-
Если при x → b функция f(x) является бесконечно большой порядка p по сравнению с
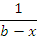 , то интерграл (2) при p < 1 сходится, а при p ≥ 1 - расходится. , то интерграл (2) при p < 1 сходится, а при p ≥ 1 - расходится.
Например, функция  при x → 1 является бесконечно большой порядка 1/3 по сравнению с при x → 1 является бесконечно большой порядка 1/3 по сравнению с 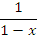 : :
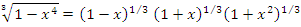 .
Следовательно, интеграл  сходится. сходится.
Аналогично, интеграл 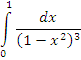 расходится, поскольку функция расходится, поскольку функция 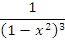 является бесконечно большой третьего порядка по сравнению с является бесконечно большой третьего порядка по сравнению с 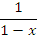 при x → 1. при x → 1.
|
 при x → 1 является бесконечно большой порядка 1/3 по сравнению с
при x → 1 является бесконечно большой порядка 1/3 по сравнению с 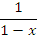 :
:
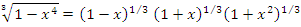 .
.
 сходится.
сходится.
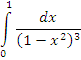 расходится, поскольку функция
расходится, поскольку функция 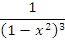 является бесконечно большой третьего порядка по сравнению с
является бесконечно большой третьего порядка по сравнению с 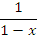 при x → 1.
при x → 1.
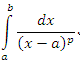
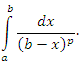
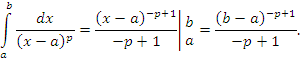
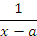 , то интерграл (1) при p < 1 сходится, а при p ≥ 1 - расходится.
, то интерграл (1) при p < 1 сходится, а при p ≥ 1 - расходится.
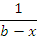 , то интерграл (2) при p < 1 сходится, а при p ≥ 1 - расходится.
, то интерграл (2) при p < 1 сходится, а при p ≥ 1 - расходится.