Признак сравнения 1.
Пусть функции f(x) и g(x) определены на промежутке (a,b) и удовлетворяют неравенству 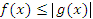 . Тогда . Тогда
1) из сходимости интеграла 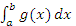 вытекает сходимость интеграла вытекает сходимость интеграла 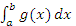 . .
2) расходимость интеграла 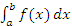 влечет за собой расходимость интеграла влечет за собой расходимость интеграла 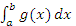 . .
Признак сравнения 2. Если существует предел 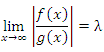 , то , то
при 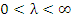 интегралы интегралы 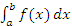 и и 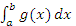 сходятся или расходятся одновременно; сходятся или расходятся одновременно;
при 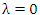 сходимость интеграла сходимость интеграла 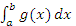 влечет за собой сходимость интеграла влечет за собой сходимость интеграла 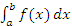 ; ;
при 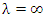 из расходимости интеграла из расходимости интеграла 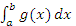 вытекает расходимость интеграла вытекает расходимость интеграла 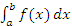 . .
|