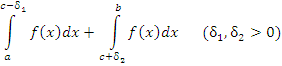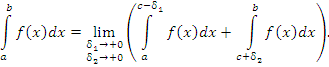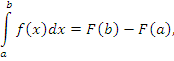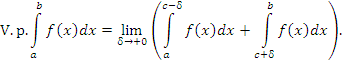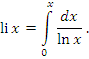|
Требование существования двойного предела функции дыух переменных (при любом способе предельного перехода) порой представляются слишком обременительными. В реальных приложениях возникают ситуации, когда условия симметрии рассматриваемой задачи снимают столь ограничительные условия.
В ситуациях подобного рода нужно либо модифицировать уже существующие понятия (например, определенного интеграла), либо расширять смысл таких понятий. |
|||||||||||||||||||||
Пусть интеграл 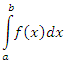 имеет единственную особенность во внутренней точке имеет единственную особенность во внутренней точке  промежутка [a,b]. Составим сумму промежутка [a,b]. Составим сумму
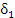 и и  . .
Если существует двойной предел выражения (1), не зависящий от способа предельного перехода, то он называется несобственным интегралом от функции f(x) по промежутку [a,b]:
Если предел (2) существует лишь при согласованном предельном переходе, а именно когда 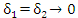 , то этот предел называется главным значением несобственного интеграла , то этот предел называется главным значением несобственного интеграла 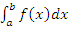 и обозначается символическим выражением и обозначается символическим выражением
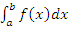 сходится в смысле главного значения. сходится в смысле главного значения.
Обозначение “V.p.” введено Коши и представляет собой аббревиатуру, которая берет свое начало от слов “Valeur principale”, означающих по-французски “Главное значение”. Любой сходящийся несобственный интеграл существует и в смысле главного значения. Обратное утверждение является неверным. Отметим, что интегралы в смысле главного значения играют важную роль в различных приложениях. Например, интегральный логарифм определяется формулой
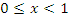 . Если же x > 1, то интеграл (5) понимается в смысле главного значения. . Если же x > 1, то интеграл (5) понимается в смысле главного значения.
|