| Introduction |
Basic Conceptions
| First-Order Differential Equations |
Directly Integrable Equations
Motion of a Body - Problem 1
Motion of a Body - Problem 2
Motion of a Body - Problem 3
The Spontaneous Radioactive of Substance
Separable Equations
Motion of Particals in Viscous Fluid
Newton's Model of Cooling
Model of Population
Separable Equations
Motion of Particals in Viscous Fluid
Newton's Model of Cooling
Model of Population
Homogeneous Equations
Linear Equations
Bernoulli Equations
Exact Differential Equations
| Differential Equations of Higher Orders |
Basic Conceptions
Equations of Special Kinds
Some Graphic Illustrations using MATLAB
| Separable Equations |
A separable differential equation is an equation of the form
![]() ,
,
We can not integrate the equation immediately because the right-hand side contains an unknown function y (x) together with the function of independent variable x.
In order to integrate this equation, it is necessary, first, to separate the factors depending on different variables, x and y:
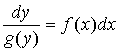 .
.
Then integrate both sides to obtain the general integral of the equation:
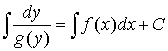 .
.
A differential equation of the form
![]()
can be reduced to a separable equation by substitution u (x) :
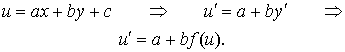
Then the general integral can be found by integration:
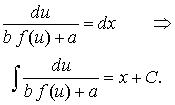
Finally, we have to solve the ordinary linear equation
u = ax + by + c
with respect to y,
![]() ,
,
substituting the result of integration for u.
|
|