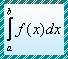| Introduction |
Basic Conceptions
| First-Order Differential Equations |
Directly Integrable Equations
Motion of a Body - Problem 1
Motion of a Body - Problem 2
Motion of a Body - Problem 3
The Spontaneous Radioactive of Substance
Separable Equations
Motion of Particals in Viscous Fluid
Newton's Model of Cooling
Model of Population
Separable Equations
Motion of Particals in Viscous Fluid
Newton's Model of Cooling
Model of Population
Homogeneous Equations
Linear Equations
Bernoulli Equations
Exact Differential Equations
| Differential Equations of Higher Orders |
Basic Conceptions
Equations of Special Kinds
Some Graphic Illustrations using MATLAB
| Real-Life Problems:
Motion of a Body - Problem 3 |
The velocity v of a moving body is the time rate of change of its position in a specified direction,
![]() . (1)
. (1)
The equality includes two time-dependent functions, s(t)
and v(t).
If v = v(t)
is a given function of t then
equality (1) is a directly integrable differential equation for the dependent
variable s = s(t), the general solution of
which has the form
![]() .
.
Let us consider a few particular cases.
- Assume that the velocity of a body is a constant value v.
Then a displacement of the body is a linear function of t:
s(t) = v t + C.The value of the constant C is determined by an initial condition, e.g. by the position of the body at time t = 0: C = s(0) = s0.
Thus,s(t) = v t + s0. - In case of a uniformly accelerated
motion of a body, the velocity is a linear function,
v(t) = a t + v0,where a is the acceleration, and v0 is an initial velocity (at t = 0).
ThenThe value of the constant C is determined by the position of the body at time point t = 0: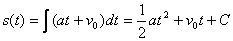 .
C = s(0) = s0.Therefore,
.
C = s(0) = s0.Therefore,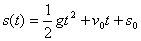 .
.
|
|