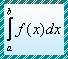| Introduction |
Basic Conceptions
| First-Order Differential Equations |
Directly Integrable Equations
Motion of a Body - Problem 1
Motion of a Body - Problem 2
Motion of a Body - Problem 3
The Spontaneous Radioactive of Substance
Separable Equations
Motion of Particals in Viscous Fluid
Newton's Model of Cooling
Model of Population
Separable Equations
Motion of Particals in Viscous Fluid
Newton's Model of Cooling
Model of Population
Homogeneous Equations
Linear Equations
Bernoulli Equations
Exact Differential Equations
| Differential Equations of Higher Orders |
Basic Conceptions
Equations of Special Kinds
Some Graphic Illustrations using MATLAB
| Basic Conceptions |
In this section we introduce the basic notation and terminology of differential equations.
The general form of a differential equation of the first order is
,
(*)
where x is the independent variable; y = y (x) is unknown function; y' is the derivative of the function.
Solution of a differential equation is a function y = y (x), which being substituted into the equation reduces it to an identity.
The general solution of equation (*)
is a function 
, which is the solution of (*)
for any values of a parameter C. If to substitute
for C some value, we obtain a particular
solution of equation (*).
Sometimes the solution can be found only in the implicit form. If the equation
,
determines the general solution of (*), then it is called the general integral of the differential equation.
If there is given an initial condition y (x0)=y0 in addition to equation (*), then it is necessary to find the particular solution which obeys the initial condition.
|
