| Definition and Properties |
The Geometric Definition of Definite Integrals
The Algebraic Definition of Definite Integrals
Properties of Definite Integrals
| Fundamental Theorems of Calculus |
The First Fundamental Theorem of Calculus
The Second Fundamental Theorem of Calculus
| Techniques of Integration |
Substitution Method
Integration by Parts
| Basic Conceptions |
| Key Topics Remaining: Algebraic Definition » Properties » The First Fundamental Theorem of Calculus » The Second Fundamental Theorem of Calculus » Substitution Method » Integration by Parts |
Problem. Let a function y = f (x) be positive defined on a closed interval [a, b]. Find the area A of the region bounded by the curve y = f (x), vertical lines x = a and x = b, and the x-axis.
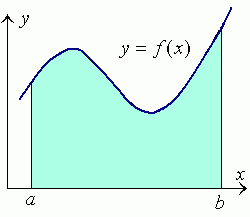
Solution.
First, divide [a, b] into n subintervals [x0,x1], [x1,x2], …, [xn-1,xn] by arbitrary points x1, x2, …, xn-1 of the partition, as it is shown in the figure below.
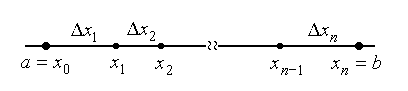
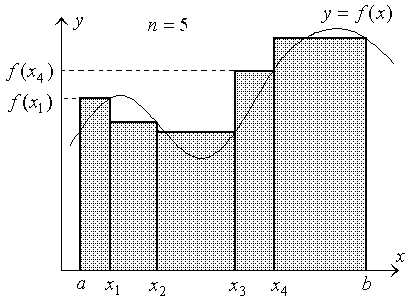
Next, draw vertical lines at the partition points and construct n rectangles as it is in the next figure. The sum of the rectangle areas approximates the area A.
![]() .
.
The heights of the constructed rectangles are equal to yk = f (xk), where the subscript k takes on integer values from 1 to n.
Taking into account that the area of each rectangle equals the product of its base and height we get
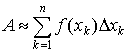 .
(*)
.
(*)In the figure below, one can easily see that approximation (*) is getting better when the number n of approximating rectangles increases.
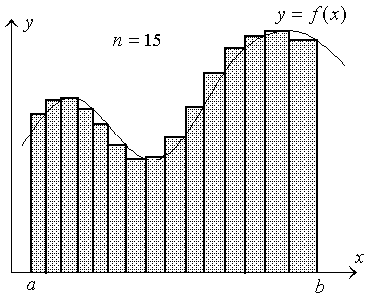
If n tends to infinity such that the bases of all rectangles tend to zero, then the area of the "staircase" figure tends to the area A.
Note that the condition "bases of all rectangles tend to zero"
can be written in a short form as "maximum 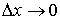 ". Therefore,
". Therefore,
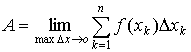 .
.
The limit of a sequence of the Riemann Sums is called the definite integral of f (x) over the interval [a, b].
Definite integrals are denoted like indefinite integrals tabbed with a and b:
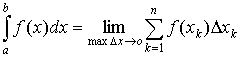 .
.
Numbers a and b are said to be the lower and upper limits of integration.