Differential Equations
Introduction

Basic Conceptions

First-Order Differential Equations

Directly Integrable Equations
  Motion of a Body - Problem 1
  Motion of a Body - Problem 2
  Motion of a Body - Problem 3
  The Spontaneous Radioactive of Substance

Separable Equations
  Motion of Particals in Viscous Fluid
  Newton's Model of Cooling
  Model of Population

Separable Equations
  Motion of Particals in Viscous Fluid
  Newton's Model of Cooling
  Model of Population

Homogeneous Equations

Linear Equations

Bernoulli Equations

Exact Differential Equations

Differential Equations of Higher Orders

Basic Conceptions
Equations of Special Kinds

Some Graphic Illustrations using MATLAB
Clich here to go to Indefinite Inegrals

Clich here to go to Definite Inegrals

Real-Life Problems:
Model of Population
Real-Life Problems:   Motion of a Body - Problem 1 » Motion of a Body - Problem 2 » Motion of a Body - Problem 3 » The Spontaneous Radioactive of Substance » Motion of Particals in Viscous Fluid » Newton's Model of Cooling » Model of Population

There exist experimental grounds that the rate of change of population is described by the following mathematical model,

.

The right-hand member consists of two terms, the first of which corresponds to a population growth with births per unit of time, and the second term represents a reduction of population with deaths. The above equation can be recognizable as a separable differential equation,

,

which implies
.

Let us transform the denominator of the integrand by making use of Partial Fractions Decomposition:

.
Therefore,
and so

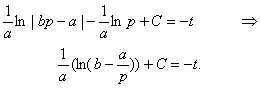
By making use of the initial condition  p(0) = p0  we find the value of the integration constant:

Thus,
that yields
or
The relative population is given by the following formula:

.

One can see that
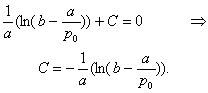
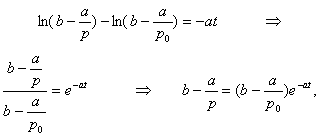
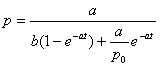
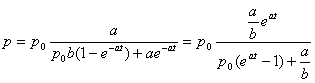
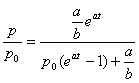p(0) = p0
and
as .
Previous Topic   Next Topic

© 2004-2010 by Norbert Grunwald and Valery Konev