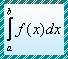Directly Integrable Equations

Differential Equations

Introduction

First-Order Differential Equations

Directly Integrable Equations
  Motion of a Body - Problem 1
  Motion of a Body - Problem 2
  Motion of a Body - Problem 3
  The Spontaneous Radioactive of Substance

Separable Equations
  Motion of Particals in Viscous Fluid
  Newton's Model of Cooling
  Model of Population

Homogeneous Equations

Linear Equations

Bernoulli Equations

Exact Differential Equations

Differential Equations of Higher Orders

Basic Conceptions
Equations of Special Kinds

Some Graphic Illustrations using MATLAB

Clich here to go to

Clich here to go to Definite Inegrals

Real-Life Problems:
The Spontaneous Radioactive of Substance

Real-Life Problems: Motion of a Body - Problem 1 » Motion of a Body - Problem 2 » Motion of a Body - Problem 3 » The Spontaneous Radioactive of Substance » Motion of Particals in Viscous Fluid » Newton's Model of Cooling » Model of Population

Let us consider a mathematical model of disintegration of a radioactive substance.
We know (due to experimental results) that the rate of radioactive decay of a substance is proportional to the quantity of the substance.
It means that

where m is the mass at some instant of time t; k is a constant, the value of which depends on the properties of the substance. The sign 'minus' says about the decay of any radioactive substance.
The above equality is a separable differential equation since it can be transformed to the form

Integration yields the general integral

If m(0) = m0 then

and so

Therefore, the partial solution has the form of exponential decay:

The coefficient k is also written in form of

. In this case, the quantity T has a special name "half-decay period", "half-life period" or "lifetime".

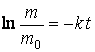Graphic Illustrations Using MATLAB.