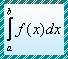Separable Equations

Differential Equations

Introduction

First-Order Differential Equations

Directly Integrable Equations
  Motion of a Body - Problem 1
  Motion of a Body - Problem 2
  Motion of a Body - Problem 3
  The Spontaneous Radioactive of Substance

Separable Equations
  Motion of Particals in Viscous Fluid
  Newton's Model of Cooling
  Model of Population

Homogeneous Equations

Linear Equations

Bernoulli Equations

Exact Differential Equations

Differential Equations of Higher Orders

Basic Conceptions
Equations of Special Kinds

Some Graphic Illustrations using MATLAB

Clich here to go to

Clich here to go to Definite Inegrals

Real-Life Problems:
Motion of Particals in Viscous Fluid

Real-Life Problems: Motion of a Body - Problem 1 » Motion of a Body - Problem 2 » Motion of a Body - Problem 3 » The Spontaneous Radioactive of Substance » Motion of Particals in Viscous Fluid » Newton's Model of Cooling » Model of Population

Let a particle move in some viscous fluid, the resisting force of medium is proportional to the velocity of the particle and it has the opposite direction with respect to the direction of movement of the particle. In view of the force of gravity, the Newton's law of motion has a form

A separable differential equation,

is easily integrated:

Substitution of t = 0 yields

where v0 = v(0).
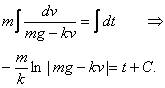
Therefore,

By making use of simple algebraic transformations we obtain

If to denote

then we obtain

Substitution for g = 10 yields

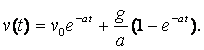
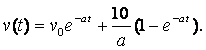
Note that v(t) approaches a limit 10 / a as t tends to infinity.

Graphic Illustrations Using MATLAB.