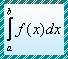A linear differential equation is an equation, which can be expressed as

,

where  P (x) and  Q (x) are given functions.

To solve the equation, introduce a new dependent variable  u(x)  instead of  y by the equality

y = u(x)v(x),

where  v(x)  is an auxiliary function.

To derive the differential equation for u(x), find the derivative

and substitute it into the given equation:

.

Next, group the terms and take out the common factor:

.       (*)

Let  v(x) be a function such that

,

which implies

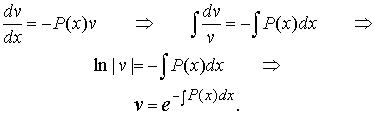
Then equation (*) is reduced to a directly integrable equation of the form

,

where

is a primitives of  P(x).

Therefore,

,

and so we obtain the general solution of the given equation:

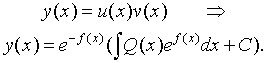
Indefinite Integrals Definite Integrals Differential Equations