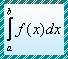| Introduction |
Basic Conceptions
| First-Order Differential Equations |
Directly Integrable Equations
Motion of a Body - Problem 1
Motion of a Body - Problem 2
Motion of a Body - Problem 3
The Spontaneous Radioactive of Substance
Separable Equations
Motion of Particals in Viscous Fluid
Newton's Model of Cooling
Model of Population
Homogeneous Equations
Linear Equations
Bernoulli Equations
Exact Differential Equations
| Differential Equations of Higher Orders |
Basic Conceptions
Equations of Special Kinds
Some Graphic Illustrations using MATLAB
| Differential Equations of Special Kinds |
1. Equations of the form
y(n) = f (x)
are easily solved by direct integration.
Really,
![]() ,
,
where f1 (x) is a primitive of f (x).
Then
![]() ,
,
and so on.
2. Let us consider equations
![]() ,
,
which do not contain the function itself and its first (k – 1) derivatives.
Applying the substitution
![]() ,
,
we obtain the equation of (n-k)-th order,
![]() ,
,
the solving of which is a simpler problem.
Let us assume that
![]()
is the general solution of the obtained equation.
Then
![]()
is a directly integrable differential equation considered above.
3. If an equation does not contain (in explicit form) the variable x,
![]() ,
,
then by making use of substitution
![]()
we have
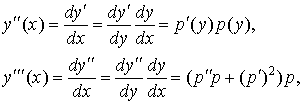
and so on.
Therefore, the original equation of the n-th order is reduced to an equation of the order (n – 1). If
![]()
is the general solution of the obtained equation, then
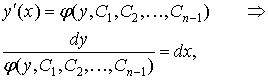
which is a differential equation with separated variables.
|
|