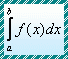| Basic Conceptions |
Primitives and Indefinite Integrals
Properties of Integrals
| Properties: Explanatory Comments |
Transformation of a Table of Common Derivatives to a Table of Integrals
A Table of Common Integrals
| Integration |
Techniques of Integration
| Integration by Substitution | ||
| ||
|
Integration by Parts |
| Integration of Rational Functions |
Basic Conceptions
Integration of Partial Fractions
Partial Fraction Decomposition
| Integration of Irrational Expressions |
Integrals Involving Rational Exponents
Integrals Involving Radicals
| Summary |
Extended List of Common Integrals
| Primitives and Indefinite Integrals |
Integrals, together with Derivatives, are the basic objects of Calculus. Indefinite integrals are defined through Primitives (or Antiderivatives).
A function F(x) is called a primitive (or antiderivative) of f (x) if
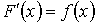
for all x in the domain of f (x).
Primitives have the following important property.
|
Let F1(x) and F2(x) be primitives of f, that is,
Then there exists a constant C such that F1(x) = F2(x) + C. |
Indeed, ![]() by definition.
by definition.
Therefore, the derivative of the difference between functions F1(x)
and F2(x) is equal to zero for all x
on the given interval:
![]() .
.
Hence, the difference F1(x) – F2(x) equals a constant by the corollary to the Mean Value Theorem.
If a function f (x) has one primitive F(x), then it has an infinite number of primitives. The set of all primitives can be expressed as F(x) + C, where C is an arbitrary constant.
The set of all primitives of f (x) is called the indefinite integral of f (x) with respect to x.
| if and only if
|
The function f (x) under the integral sign is called the integrand.
The x is the integration variable.
The symbol dx is the differential of x.
An arbitrary constant C is said to be a constant of integration.
Note that solutions of differential equations can be expressed in terms of indefinite integral. For example,
 .
.