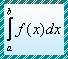Directly Integrable Equations

Differential Equations

Introduction

First-Order Differential Equations

Directly Integrable Equations
  Motion of a Body - Problem 1
  Motion of a Body - Problem 2
  Motion of a Body - Problem 3
  The Spontaneous Radioactive of Substance

Separable Equations
  Motion of Particals in Viscous Fluid
  Newton's Model of Cooling
  Model of Population

Homogeneous Equations

Linear Equations

Bernoulli Equations

Exact Differential Equations

Differential Equations of Higher Orders

Basic Conceptions
Equations of Special Kinds

Some Graphic Illustrations using MATLAB

Clich here to go to

Clich here to go to Definite Inegrals

Real-Life Problems:
Motion of a Body - Problem 1

Real-Life Problems: Motion of a Body - Problem 1 » Motion of a Body - Problem 2 » Motion of a Body - Problem 3 » The Spontaneous Radioactive of Substance » Motion of Particals in Viscous Fluid » Newton's Model of Cooling » Model of Population

The Newton's law of motion equates the time rate of change of particle momentum p = m v and the resultant force F applied to the particle:

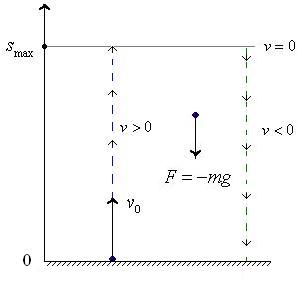
Let us consider a motion of a body thrown straight upward with a velocity v0.

If to neglect by the air drag then the only actual force is the force of Earth's attraction, the value of which is equal to the product of the mass m of the body and the acceleration of gravity

; the force direction is opposite to the initial moving direction of the body. A mathematical model of motion can be represented by the following initial value problem:

Then integration yields the general solution:

v(t) = –g t +C.

Substitution of t = 0 gives the value of the constant of integration:

C = v(0) = v0.

Thus, we obtain the particular solution:

v(t) = v0 – g t.

The body reaches its maximum height when v(t) = 0, that is, at the time point

t = v0 / g.

Graphic Illustrations Using MATLAB.