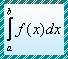| Introduction |
Basic Conceptions
| First-Order Differential Equations |
Directly Integrable Equations
Motion of a Body - Problem 1
Motion of a Body - Problem 2
Motion of a Body - Problem 3
The Spontaneous Radioactive of Substance
Separable Equations
Motion of Particals in Viscous Fluid
Newton's Model of Cooling
Model of Population
Separable Equations
Motion of Particals in Viscous Fluid
Newton's Model of Cooling
Model of Population
Homogeneous Equations
Linear Equations
Bernoulli Equations
Exact Differential Equations
| Differential Equations of Higher Orders |
Basic Conceptions
Equations of Special Kinds
Some Graphic Illustrations using MATLAB
| Real-Life Problems:
Motion of a Body - Problem 2 |
Let a body be thrown straight downward from some height
with a velocity v0.
In this case, a mathematical model of motion is represented by the following
IVP,
the particular solution of which is
v(t)
= g t +C.
One can see that the speed of the body increases infinitely as t tends to infinity.
Such conclusion conflicts with experimental data and therefore, it is necessary to refine
the mathematical model in order to broaden the area of its application.
Click here to see a more realistic model.
|
|