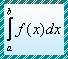The Bernoulli Equations

Differential Equations

Introduction

Basic Conceptions

First-Order Differential Equations

Differential Equations of Higher Orders

The Bernoulli Equations

The Bernoulli Equation is a differential equation of the form

where n is any rational number except for 0 and 1.

The technique of solving Bernoulli equations is just the same as that of linear equations.

Let us introduce a new dependent variable u(x) by means of the equality

y = u(x)v(x).

This variable satisfies the equation

where the function v(x) is a particular solution of the equation

and hence,

Then the equation for u(x) is transformed to the following form

which can be rewritten as a separable equation,

By integrating, we obtain

Thus,

and the general solution of the given equation is

y = u(x)v(x).