| Introduction |
Basic Conceptions
| First-Order Differential Equations |
Directly Integrable Equations
Motion of a Body - Problem 1
Motion of a Body - Problem 2
Motion of a Body - Problem 3
The Spontaneous Radioactive of Substance
Separable Equations
Motion of Particals in Viscous Fluid
Newton's Model of Cooling
Model of Population
Homogeneous Equations
Linear Equations
Bernoulli Equations
Exact Differential Equations
| Differential Equations of Higher Orders |
Basic Conceptions
Equations of Special Kinds
Some Graphic Illustrations using MATLAB
| Exact Differential Equations |
An exact differential equation has the following form
![]() , (1)
, (1)
where the partial derivatives of P(x,y) and Q(x,y) obey the condition
![]() .
(2)
.
(2)
Due to condition (2) and in view of the theorem of a total differential, the expression on the left-hand side of equation (1) is the total differential of some function u(x,y):
![]() .
.
Therefore,
![]() , (3)
, (3)
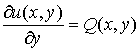 , (4)
, (4)
and
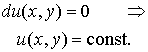
If we hold y fixed, then by integrating equation (3) with respect to x, we obtain
![]() .
(5)
.
(5)
Note that constant of integration ![]() depends on the variable y
because y is considered as a constant in
the integral with respect to x.
depends on the variable y
because y is considered as a constant in
the integral with respect to x.
To find ![]() , substitute expression (5)
into equation (4):
, substitute expression (5)
into equation (4):
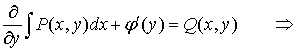
This is an ordinary differential equation for the function ![]() .
.
Since ![]() depends on the variable y
only, the expression on the right-hand side of (4) must also be a function
of y only. Otherwise, equation (1) is not
an exact differential equation.
depends on the variable y
only, the expression on the right-hand side of (4) must also be a function
of y only. Otherwise, equation (1) is not
an exact differential equation.
By solving equation (6), we find a particular solution
![]() and hence, the general integral
and hence, the general integral
u(x,y) = C.
|
|
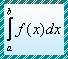
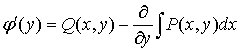 . (6)
. (6)