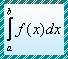| Introduction |
Basic Conceptions
| First-Order Differential Equations |
Directly Integrable Equations
Motion of a Body - Problem 1
Motion of a Body - Problem 2
Motion of a Body - Problem 3
The Spontaneous Radioactive of Substance
Separable Equations
Motion of Particals in Viscous Fluid
Newton's Model of Cooling
Model of Population
Homogeneous Equations
Linear Equations
Bernoulli Equations
Exact Differential Equations
| Differential Equations of Higher Orders |
Basic Conceptions
Equations of Special Kinds
Some Graphic Illustrations using MATLAB
| Differential Equations of Higher Orders |
An implicit differential equation of n-th order can be written as
. (*)
An explicit differential equation of n-th order has the following form:
. (**)
The general solution of equation (*) or (**) is a function
,
which satisfies the equation for any allowable set of the constants 
.
A chosen numerical set of the constants gives a particular solution.
Cauchy Problem: Find a particular solution of a differential equation, that satisfies the given initial conditions (i.e., solve the initial value problem),
(***)
To solve a differential equation means:
(i) to find the general solution
or
(ii) to solve the Cauchy problem.
Existence and Unicity Theorem. If the function
and its partial derivatives
are continuous functions in some domain D
that includes the point
then there exists a unique solution of equation (**) that satisfies the initial conditions (***).
|
