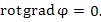Векторное поле A, ротор которого равен нулю, называется безвихревым. В этом случае
| |
 .
|
(1) |
|
Заметим, что условия (1) совпадают с условиями потенциальности поля A. Это означает, что существует скалярное поле  , градиент которого равен A:
Таким образом, уравнение , градиент которого равен A:
Таким образом, уравнение 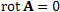 выражает условие потенциальности поля A. Следовательно, всякое безвихревое поле является потенциальным. выражает условие потенциальности поля A. Следовательно, всякое безвихревое поле является потенциальным.
 Справедливо и обратное утверждение: всякое потенциальное поле является безвихревым. Действительно, потенциальность поля A влечет за собой равенство нулю циркуляции вектора A по любому контуру L , расположенному в области непрерывности поля:
Справедливо и обратное утверждение: всякое потенциальное поле является безвихревым. Действительно, потенциальность поля A влечет за собой равенство нулю циркуляции вектора A по любому контуру L , расположенному в области непрерывности поля:
 .
Тогда из теоремы Стокса
|
Теорема Стокса
Циркуляция векторного поля A по замкнутому контуру L равна потоку ротора A через поверхность S, натянутую на контур L :
|
следует, что равен нулю и поток ротора A через любую натянутую на контур L поверхность. Учитывая произвольность формы и размеров этой поверхности, мы должны заключить, что 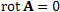 . .
 Таким образом, для любого скалярного поля
Таким образом, для любого скалярного поля 
 В заключение отметим, что любое векторное поле можно представить в виде суммы безвихревого и соленоидального полей.
В заключение отметим, что любое векторное поле можно представить в виде суммы безвихревого и соленоидального полей.
|
 , градиент которого равен A:
, градиент которого равен A:
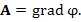
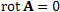 выражает условие потенциальности поля A. Следовательно, всякое безвихревое поле является потенциальным.
выражает условие потенциальности поля A. Следовательно, всякое безвихревое поле является потенциальным.
 .
.
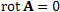 .
.

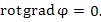
 , градиент которого равен A:
, градиент которого равен A:
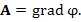
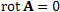 выражает условие потенциальности поля A. Следовательно, всякое безвихревое поле является потенциальным.
выражает условие потенциальности поля A. Следовательно, всякое безвихревое поле является потенциальным.
 .
.
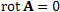 .
.