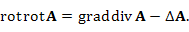Результатом применения оператора набла к скалярному полю 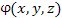 является векторное поле является векторное поле  К этому полю можно вновь применить оператор набла, используя операцию скалярного или векторного произведения:
Если чисто формально воспринимать векторный оператор К этому полю можно вновь применить оператор набла, используя операцию скалярного или векторного произведения:
Если чисто формально воспринимать векторный оператор  как обычный вектор, то с точки зрения векторной алгебры произведение как обычный вектор, то с точки зрения векторной алгебры произведение  (равных друг другу векторов) должно равняться нулю. Однако алгебра векторных операторов далеко не всех отношениях совпадает с алгеброй векторов; между ними имеются и существенные различия. Например, (равных друг другу векторов) должно равняться нулю. Однако алгебра векторных операторов далеко не всех отношениях совпадает с алгеброй векторов; между ними имеются и существенные различия. Например,  если если 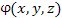 и частные производные и частные производные  представляют собой непрерывные функции. В противном случае
Таким образом, уравнение представляют собой непрерывные функции. В противном случае
Таким образом, уравнение 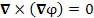 не является тождеством, а удовлетворяется только для определенного класса функций не является тождеством, а удовлетворяется только для определенного класса функций 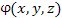 . .
 Можно образовать четыре дифференциальных операции второго порядка, если повторно применить оператор набла к выражениям вида
Тогда
При выполнении соответствующих условий непрерывности векторного поля A,
Можно образовать четыре дифференциальных операции второго порядка, если повторно применить оператор набла к выражениям вида
Тогда
При выполнении соответствующих условий непрерывности векторного поля A, 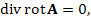 тогда как ротор ротора A можно представить в виде
Доказательство последнего утверждения предоставляется читателю. тогда как ротор ротора A можно представить в виде
Доказательство последнего утверждения предоставляется читателю.
|
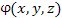 является векторное поле
является векторное поле  К этому полю можно вновь применить оператор набла, используя операцию скалярного или векторного произведения:
К этому полю можно вновь применить оператор набла, используя операцию скалярного или векторного произведения:
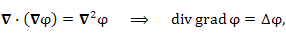
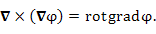
 как обычный вектор, то с точки зрения векторной алгебры произведение
как обычный вектор, то с точки зрения векторной алгебры произведение  (равных друг другу векторов) должно равняться нулю. Однако алгебра векторных операторов далеко не всех отношениях совпадает с алгеброй векторов; между ними имеются и существенные различия. Например,
(равных друг другу векторов) должно равняться нулю. Однако алгебра векторных операторов далеко не всех отношениях совпадает с алгеброй векторов; между ними имеются и существенные различия. Например,  если
если 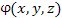 и частные производные
и частные производные  представляют собой непрерывные функции. В противном случае
представляют собой непрерывные функции. В противном случае
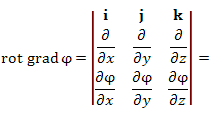
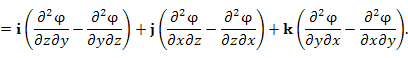
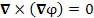 не является тождеством, а удовлетворяется только для определенного класса функций
не является тождеством, а удовлетворяется только для определенного класса функций 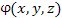 .
.
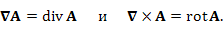
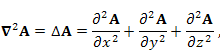

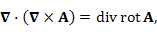
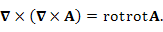
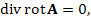 тогда как ротор ротора A можно представить в виде
тогда как ротор ротора A можно представить в виде