Координаты представляют собой величины, определяющие положение какого-либо элемента (например, точки) на плоскости, в пространстве или на ином многообразии. Необходимое число таких величин определяется размерностью пространства. Координаты вектора называют его компонентами.
 , если каждой точке M этого пространства поставлен во взаимно однозначное соответствие набор чисел , если каждой точке M этого пространства поставлен во взаимно однозначное соответствие набор чисел 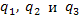 . (Различным тройкам чисел . (Различным тройкам чисел 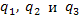 соответствуют различные точки пространства). В качестве таких чисел могут выступать декартовы координаты, цилиндрические координаты, сферические координаты и так далее. В общем случае числа соответствуют различные точки пространства). В качестве таких чисел могут выступать декартовы координаты, цилиндрические координаты, сферические координаты и так далее. В общем случае числа 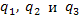 называются криволинейными координатами точки М. называются криволинейными координатами точки М.
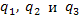 образован проекциями точки M на три взаимно перпендикулярные оси 0x, 0y и 0z. Декартовы координаты точки обозначаются символами x, y и z. образован проекциями точки M на три взаимно перпендикулярные оси 0x, 0y и 0z. Декартовы координаты точки обозначаются символами x, y и z.
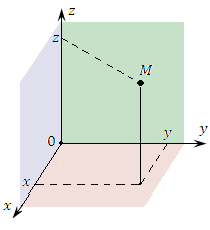
Рис. 1. Декартовы координаты точки M. 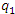 , а остальные координаты остаются неизменными, называется координатной , а остальные координаты остаются неизменными, называется координатной 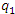 -линией. -линией.
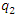 и и 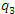 -линии. -линии.

Рис. 2. Координатные линии двухмерной системы криволинейных координат. 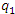 -линии в точке М, направленный в сторону возрастания координаты -линии в точке М, направленный в сторону возрастания координаты 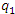 , называется единичным ортом , называется единичным ортом 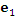 в точке М. в точке М.
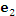 и и 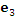 . .
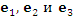 попарно ортогональны. попарно ортогональны.
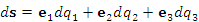 : :
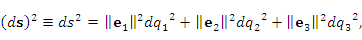
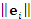 – норма (длина) вектора – норма (длина) вектора 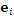 . .
|