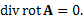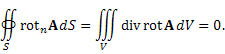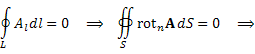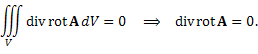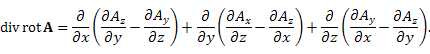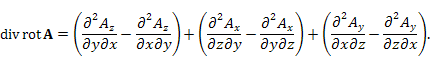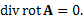Конев В.В.  Скалярные и векторные поля

| Словарь | Калькулятор | Тесты | Задачи и упражнения |
| Скалярные и векторные поля. Градиент | Циркуляция. Поток. Дивергенция |
Теорема о равенстве нулю дивергенции ротора
Теорема. Для любого дважды дифференцируемого векторного поля A поле ротора  A  является соленоидальным:
Доказательство 1. Пусть на малый контур  L  натянута некоторая поверхность  S , показанная на рисунке 1.

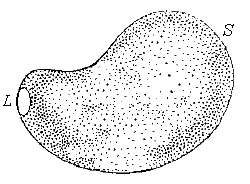Рис. 1. При стягивании контура  L  в точку граница поверхности исчезает, а поверхность становится замкнутой.
     Если векторное поле  A  конечно в области, ограниченной контуром  L , то циркуляция  A  по контуру  L  стремится к нулю по мере стягивания контура в точку. Тогда по теореме Стокса
     Согласно теореме Остроградского-Гаусса, поток векторного поля через замкнутую поверхность равен тройному интегралу от дивергенции этого поля. Следовательно,
      В виду произвольности области интнгрирования равенство нулю интеграла влечет за собой равенство нулю подынтегральной функции в любой точке пространства.
     Таким образом, для любого векторного поля  A
Доказательство 2. Выберем произвольную замкнутую гладкую поверхность  S  и окружим ее контуром, изображенным на рисунке 2.

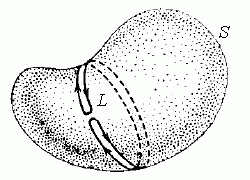Рис. 2. Поверхность  S, окруженная замкнутой кривой  L.
Циркуляция векторного поля  A  по контуру  L  равна нулю, что согласно теореме Стокса влечет равенство нулю потока ротора  A  через замкнутую поверхность  S. Тогда – в силу теореиы Остроградского-Гаусса – равен нулю и тройной интеграл от дивергенции ротора  A  по области, ограниченной поверхностью  S.

Ссылка на произвольность области интегрирования завершает доказательство.
Доказательство 3. Найдем дивергенцию ротора векторного поля прямым вычислением.
Перегруппировывая слагаемые, получим
Если векторное поле A и его частные производные являются непрерывными функциями, то смешанные произыоднве не зависят от порядка дифференцирования и, следовательно,