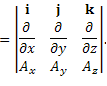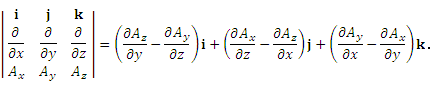Проекция ротора векторного поля A в точке 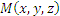 на направление нормали к поверхности, натянутой на контур ΔL, определяется формулой на направление нормали к поверхности, натянутой на контур ΔL, определяется формулой
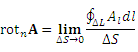 ,
где  – циркуляция вектора A вдоль контура ΔL; ΔS – площадь области, ограниченной этим контуром. – циркуляция вектора A вдоль контура ΔL; ΔS – площадь области, ограниченной этим контуром.
Теорема. В прямоугольной системе координат ротор вектора A можно представить в виде
где Ax, Ay и Az – координаты вектора A . В прямоугольной системе координат ротор вектора A можно представить в виде
где Ax, Ay и Az – координаты вектора A .
Доказательство. Выберем в качестве контура интегрирования ΔL границу бесконечно малого прямоугольника, расположенного в плоскости, параллельной координатной плоскости x0y (как это показано на рисунке 1). Выберем в качестве контура интегрирования ΔL границу бесконечно малого прямоугольника, расположенного в плоскости, параллельной координатной плоскости x0y (как это показано на рисунке 1).
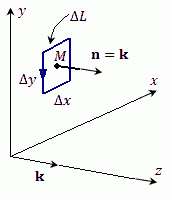 Рис. 1
Рис. 1. Контур интегрирования Δ L представляет собой прямоугольник, центром которого является точка 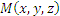 .
 Площадь ΔS такого прямоугольника равна Δx · Δy, а направление его нормали совпадает с положительным направлением оси z.
Площадь ΔS такого прямоугольника равна Δx · Δy, а направление его нормали совпадает с положительным направлением оси z.
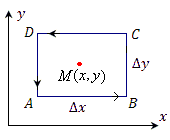 Рис. 2
Рис. 2. Контур интегрирования.
 Следовательно, отношение циркуляции
Следовательно, отношение циркуляции  к площади ΔS при стягивании контура в точку дает z-компоненту ротора. к площади ΔS при стягивании контура в точку дает z-компоненту ротора.
 Представим циркуляцию векторного поля A в виде суммы интегралов:
Представим циркуляцию векторного поля A в виде суммы интегралов:
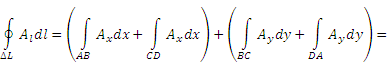
 .
Учитывая малость сторон прямоугольника, функции Ax и Ay можно заменить их средними значениями на соответствующих отрезках. Заметим, однако, что значение проекции Ax на отрезке DC отличается от соответствующего значения на отрезке AB на величину 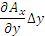 . .
Тогда
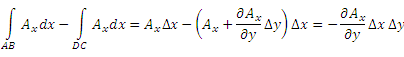 .
Аналогично, разность значений Ay на отрезках BC и AD составляет 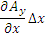 . Следовательно, . Следовательно,
 .
Таким образом,
 .
Принимая во внимание предельное соотношение
 ,
приходим к формуле
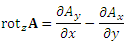 .
Выражения для других координат ротора могут быть получены с помощью циклической замены переменных 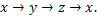 :
Представление ротора в терминах оператора набла. :
Представление ротора в терминах оператора набла.
Рассмотрим векторное произведение оператора векторное произведение оператора 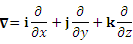 и векторной функции и векторной функции  :
Преобразуем это выражение, применяя теорему о разложении определителя по элементам строки. (Напомним, что операторы дифференцирования должны всегда располагаться слева от функций, на которые они действуют.)
Полученный результат совпадает с выражением для ротора векторного поля A. Следовательно, :
Преобразуем это выражение, применяя теорему о разложении определителя по элементам строки. (Напомним, что операторы дифференцирования должны всегда располагаться слева от функций, на которые они действуют.)
Полученный результат совпадает с выражением для ротора векторного поля A. Следовательно,
|
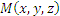 на направление нормали к поверхности, натянутой на контур ΔL, определяется формулой
на направление нормали к поверхности, натянутой на контур ΔL, определяется формулой
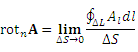 ,
,  – циркуляция вектора A вдоль контура ΔL; ΔS – площадь области, ограниченной этим контуром.
– циркуляция вектора A вдоль контура ΔL; ΔS – площадь области, ограниченной этим контуром.
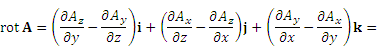
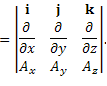

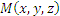 .
. 
 к площади ΔS при стягивании контура в точку дает z-компоненту ротора.
к площади ΔS при стягивании контура в точку дает z-компоненту ротора.
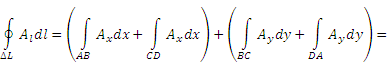
 .
.
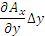 .
.
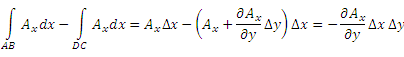 .
.
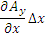 . Следовательно,
. Следовательно,
 .
.
 .
.
 ,
,
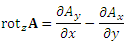 .
.
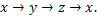 :
:
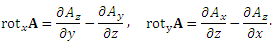
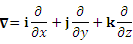 и векторной функции
и векторной функции  :
: