Цилиндрическая система координат представляет собой трёхмерную систему координат, являющуюся обобщением полярной системы координат посредством добавления третьей координаты, которая задаёт смещение произвольной точки M вдоль оси 0z относительно координатной плоскости 0xy. Положение точки M в цилиндрической системе координат определяется тройкой чисел ρ, φ и z, где ρ – расстояние от точки M до оси 0z ( ); φ – угол, образованный проекцией радиус-вектора точки M на плоскость 0ху с положительным направлением оси 0х ( ); φ – угол, образованный проекцией радиус-вектора точки M на плоскость 0ху с положительным направлением оси 0х (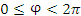 ); z – проекция точки M на ось 0z ( ); z – проекция точки M на ось 0z ( ). ).
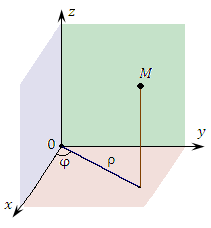 Рис. 1
Рис. 1. Цилиндрические координаты точки M.
 Связь между декартовыми и цилиндрическими координатами описывается формулами
Поверхность, на которой одна из координат сохраняет постоянное значение, называется координатной поверхностью.
Связь между декартовыми и цилиндрическими координатами описывается формулами
Поверхность, на которой одна из координат сохраняет постоянное значение, называется координатной поверхностью.
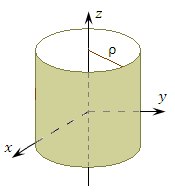 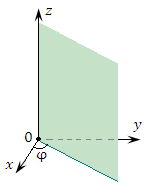 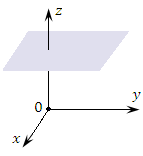 Рис. 2
Рис. 2. Координатные поверхности цилиндрической системы координат:
круговой цилиндр (ρ = const);
полуплоскость (φ = const);
плоскость ( z = const).
 Линия, вдоль которой изменяется только одна координата, а остальные координаты остаются неизменными, называется координатной линией.
Линия, вдоль которой изменяется только одна координата, а остальные координаты остаются неизменными, называется координатной линией.
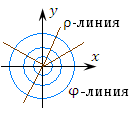 Рис. 3
Рис. 3. Координатные ρ-линии (лучи) и φ-линии (окружности) цилиндрической системы координат.
Координатная z-линия (прямая) направлена перпендикулярно плоскости 0 xy.
 В цилиндрической системе координатные линии, проходящие через любую точку M пространства, пересекаются под прямым углом. Такие системы координат называются ортогональными.
В цилиндрической системе координатные линии, проходящие через любую точку M пространства, пересекаются под прямым углом. Такие системы координат называются ортогональными.
 Единичный касательный вектор к координатной линии в точке М, направленный в сторону возрастания координаты, называется ортом в точке М. Поскольку цилиндрическая система координат является ортогональной, то в любой точке пространства векторы
Единичный касательный вектор к координатной линии в точке М, направленный в сторону возрастания координаты, называется ортом в точке М. Поскольку цилиндрическая система координат является ортогональной, то в любой точке пространства векторы 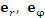 и и 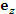 попарно ортогональны. попарно ортогональны.
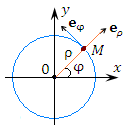 Рис. 4
Рис. 4. Орты 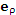 и 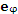 цилиндрической системы координат.
Вектор 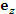 направлен перпендикулярно плоскости 0 xy.
 Отметим, что каждая координатная линия перпендикулярна соответствующей координатной поверхности.
Отметим, что каждая координатная линия перпендикулярна соответствующей координатной поверхности.
Некоторые полезные формулы:
-
Элемент длины дуги:
-
Элемент площади поверхности:
-
Якобиан перехода от декартовой системы координат к цилиндрической:
-
Элемент объема:
|