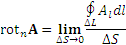Теорема. Пусть контур L является границей поверхности S, вдоль которой определена векторная функция A . Тогда циркуляция векторного поля A по замкнутому контуру L равна потоку ротора A через поверхность S, натянутую на контур L :
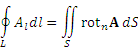 .
Доказательство. Разобъем поверхность S на малые элементы Разобъем поверхность S на малые элементы 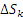 , каждый из которых представляет собой достаточно плоский участок, что соответствует разбиению контура L на петли, сумма циркуляций по которым равна циркуляции по исходному контуру.
(См. свойство циркуляции.) , каждый из которых представляет собой достаточно плоский участок, что соответствует разбиению контура L на петли, сумма циркуляций по которым равна циркуляции по исходному контуру.
(См. свойство циркуляции.)
|
Свойство циркуляции
Для вычисления циркуляции векторного поля по контуру L можно разбить область, ограниченную контуром, на малые злементы (например, прямоугольники) и просуммировать результаты интегрирования по границам элементарных областей.
|
 Рис. 1
Рис. 1. Контур L, являющийся границей некоторой поверхности S, разбивается на множество малых контуров 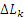 , лежащих на поверхности S.
Согласно определению ротора,
Определение ротора векторного поля
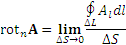
|
циркуляцию вектора A вдоль бесконечно малого контура ΔLk , являющегося границей элемента поверхности ΔSk , можно представить в виде
где 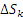 – площадь элемента – площадь элемента 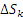 ; ; 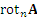 – проекция rot A на нормаль к – проекция rot A на нормаль к 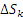 . .
 Суммирование по всем элементам дает в левой части этого равенства циркуляцию вектора A по контуру L , а в правой – интегральную сумму, соответствующую поверхностному интегралу второго рода от ротора A.
Суммирование по всем элементам дает в левой части этого равенства циркуляцию вектора A по контуру L , а в правой – интегральную сумму, соответствующую поверхностному интегралу второго рода от ротора A.
 Предельный переход, означающий разбиение контура на петли бесконечно малых размеров, обеспечивает выполнение точного равества между циркуляцией векторного поля A и потоком ротора A через поверхность, натянутую на контур.
Предельный переход, означающий разбиение контура на петли бесконечно малых размеров, обеспечивает выполнение точного равества между циркуляцией векторного поля A и потоком ротора A через поверхность, натянутую на контур.
|
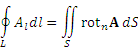 .
.
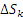 , каждый из которых представляет собой достаточно плоский участок, что соответствует разбиению контура L на петли, сумма циркуляций по которым равна циркуляции по исходному контуру.
(См. свойство циркуляции.)
, каждый из которых представляет собой достаточно плоский участок, что соответствует разбиению контура L на петли, сумма циркуляций по которым равна циркуляции по исходному контуру.
(См. свойство циркуляции.)

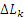 , лежащих на поверхности S.
, лежащих на поверхности S. 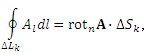
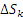 – площадь элемента
– площадь элемента 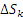 ;
; 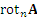 – проекция rot A на нормаль к
– проекция rot A на нормаль к 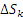 .
.