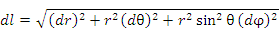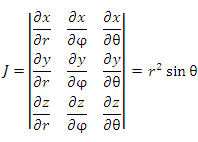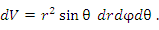Положение точки М в сферической системе координат задается тройкой чисел r, φ и θ, где r – расстояние от начала координат до точки M (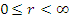 ); φ – угол, образованный проекцией радиус-вектора точки M на плоскость 0ху с положительным направлением оси 0х ( ); φ – угол, образованный проекцией радиус-вектора точки M на плоскость 0ху с положительным направлением оси 0х (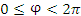 ); θ – угол между положительным направлением оси Oz и радиус-вектором точки М ( ); θ – угол между положительным направлением оси Oz и радиус-вектором точки М (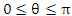 ). ).
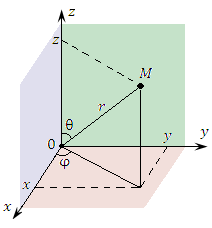 Рис. 1
Рис. 1. Сферические координаты точки M.
 Связь между декартовыми и сферическими координатами описывается формулами
Связь между сферическими и цилиндрическими координатами описывается формулами
Связь между декартовыми и сферическими координатами описывается формулами
Связь между сферическими и цилиндрическими координатами описывается формулами
 Поверхность, на которой одна из координат сохраняет постоянное значение, называется координатной поверхностью.
Поверхность, на которой одна из координат сохраняет постоянное значение, называется координатной поверхностью.
 Линия, вдоль которой изменяется только одна координата, а остальные координаты остаются неизменными, называется координатной линией.
Линия, вдоль которой изменяется только одна координата, а остальные координаты остаются неизменными, называется координатной линией.
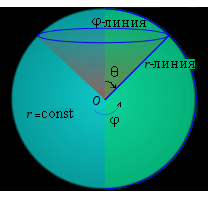 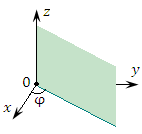 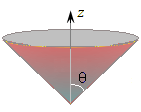 Рис. 2
Рис. 2. Координатные поверхности сферической системы координат:
сфера ( r = const);
полуплоскость (φ = const);
конус (θ = const).
 В сферической системе координатные линии, проходящие через любую точку M пространства, пересекаются под прямым углом. Такие системы координат называются ортогональными.
В сферической системе координатные линии, проходящие через любую точку M пространства, пересекаются под прямым углом. Такие системы координат называются ортогональными.
 Единичный касательный вектор к координатной линии в точке М, направленный в сторону возрастания координаты, называется ортом в точке М. Поскольку сферическая система координат является ортогональной, то в любой точке пространства векторы
Единичный касательный вектор к координатной линии в точке М, направленный в сторону возрастания координаты, называется ортом в точке М. Поскольку сферическая система координат является ортогональной, то в любой точке пространства векторы 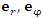 и и 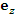 попарно ортогональны. попарно ортогональны.
 Отметим, что каждая координатная линия перпендикулярна соответствующей координатной поверхности.
Отметим, что каждая координатная линия перпендикулярна соответствующей координатной поверхности.
Некоторые полезные формулы:
-
Элемент длины дуги:
-
Якобиан перехода от декартовой системы координат к сферической:
-
Элемент объема:
|
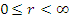 ); φ – угол, образованный проекцией радиус-вектора точки M на плоскость 0ху с положительным направлением оси 0х (
); φ – угол, образованный проекцией радиус-вектора точки M на плоскость 0ху с положительным направлением оси 0х (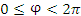 ); θ – угол между положительным направлением оси Oz и радиус-вектором точки М (
); θ – угол между положительным направлением оси Oz и радиус-вектором точки М (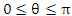 ).
).

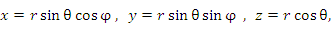
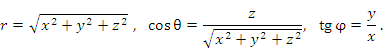
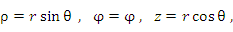
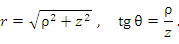



 и
и 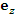 попарно ортогональны.
попарно ортогональны.