Теорема. Циркуляция векторного поля 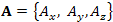 вдоль замкнутого контура L равна потоку ротора A через поверхность S, натянутую на контур L : вдоль замкнутого контура L равна потоку ротора A через поверхность S, натянутую на контур L :
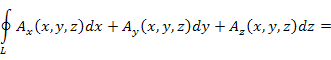
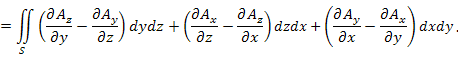
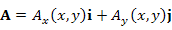
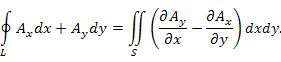
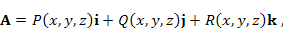
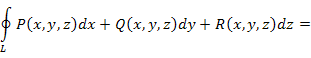
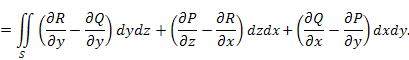
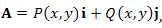
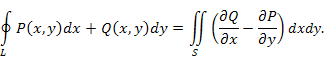
|
Теорема. Циркуляция векторного поля 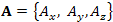 вдоль замкнутого контура L равна потоку ротора A через поверхность S, натянутую на контур L : вдоль замкнутого контура L равна потоку ротора A через поверхность S, натянутую на контур L :
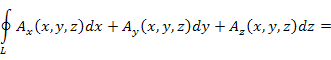
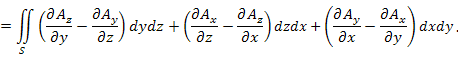
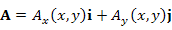
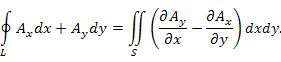
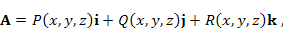
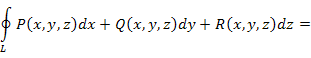
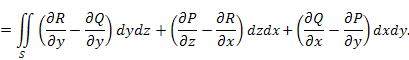
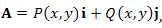
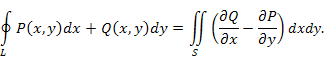
|