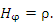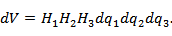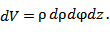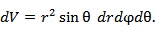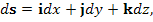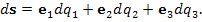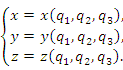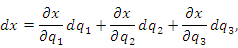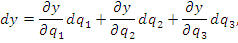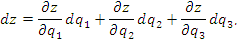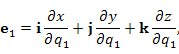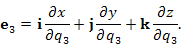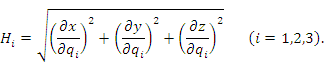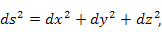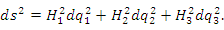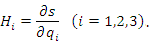Пусть в трехмерном пространстве задана система координат 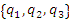 . Представим бесконечно малый вектор ds в виде разложения по декартовому базису векторов i, j, k и по базисному набору векторов . Представим бесконечно малый вектор ds в виде разложения по декартовому базису векторов i, j, k и по базисному набору векторов 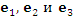 криволинейной системы координат криволинейной системы координат 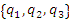 : :
 Для того, чтобы величины
Для того, чтобы величины 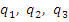 могли рассматриваться в качестве координат элемента в некоторой области пространства, необходимо существование обратного отображения могли рассматриваться в качестве координат элемента в некоторой области пространства, необходимо существование обратного отображения
| |
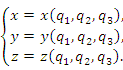
|
(3) |
|
 Выразим в уравнении (1) дифференциалы декартовых координат через дифференциалы криволинейных координат:
Тогда
Выразим в уравнении (1) дифференциалы декартовых координат через дифференциалы криволинейных координат:
Тогда
 Если система координат
Если система координат 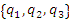 ортогональна, то в любой точке пространства векторы ортогональна, то в любой точке пространства векторы 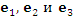 попарно ортогональны:
где попарно ортогональны:
где 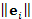 - норма вектора - норма вектора 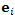 (длина вектора); (длина вектора);  - дельта-символ Кронекера, определяемый формулой - дельта-символ Кронекера, определяемый формулой
 Норму вектора
Норму вектора 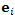 называют также коэффициентом Ламе называют также коэффициентом Ламе 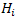 для координаты для координаты 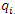 в точке М: в точке М:
| |
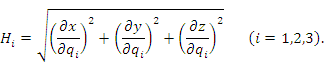
|
(6) |
|
Из формул (1) и (2) следует, что в ортогональной системе координат квадрат дифференциала длины дуги произвольной кривой может быть представлен в виде
| |
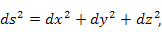
|
(7) |
|
| |
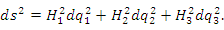
|
(8) |
|
 Если фиксировать две координаты из набора
Если фиксировать две координаты из набора 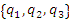 , то равенство (7) приводит к следующей формуле для коэффициентов Ламе: , то равенство (7) приводит к следующей формуле для коэффициентов Ламе:
| |
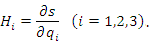
|
(9) |
|
В результате мы получаем другой спосов вычисления коэффициентов Ламе 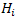 , в соответствии с которым достаточно записать отношение длины дуги бесконечно малого элемента координатной , в соответствии с которым достаточно записать отношение длины дуги бесконечно малого элемента координатной 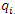 -линии к дифференциалу координаты -линии к дифференциалу координаты 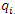 . Например, в цилиндрической системе координатными ρ- и z-линиями являются полупрямая и прямая соответственно, что влечет . Например, в цилиндрической системе координатными ρ- и z-линиями являются полупрямая и прямая соответственно, что влечет 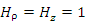 . Поскольку координатной . Поскольку координатной 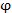 -линией является окружность радиуса ρ, то -линией является окружность радиуса ρ, то 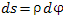 и и 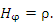
 Элемент объема в криволинейных координатах определяется формулой
Тогда в цилиндрической системе координат
В сферической системе координат
Элемент объема в криволинейных координатах определяется формулой
Тогда в цилиндрической системе координат
В сферической системе координат
|
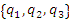 . Представим бесконечно малый вектор ds в виде разложения по декартовому базису векторов i, j, k и по базисному набору векторов
. Представим бесконечно малый вектор ds в виде разложения по декартовому базису векторов i, j, k и по базисному набору векторов 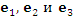 криволинейной системы координат
криволинейной системы координат 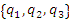 :
:
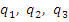 могли рассматриваться в качестве координат элемента в некоторой области пространства, необходимо существование обратного отображения
могли рассматриваться в качестве координат элемента в некоторой области пространства, необходимо существование обратного отображения
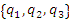 ортогональна, то в любой точке пространства векторы
ортогональна, то в любой точке пространства векторы 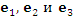 попарно ортогональны:
попарно ортогональны:
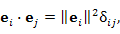
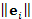 - норма вектора
- норма вектора 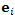 (длина вектора);
(длина вектора);  - дельта-символ Кронекера, определяемый формулой
- дельта-символ Кронекера, определяемый формулой
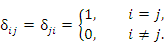
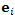 называют также коэффициентом Ламе
называют также коэффициентом Ламе 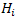 для координаты
для координаты 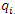 в точке М:
в точке М:
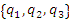 , то равенство (7) приводит к следующей формуле для коэффициентов Ламе:
, то равенство (7) приводит к следующей формуле для коэффициентов Ламе:
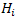 , в соответствии с которым достаточно записать отношение длины дуги бесконечно малого элемента координатной
, в соответствии с которым достаточно записать отношение длины дуги бесконечно малого элемента координатной 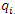 -линии к дифференциалу координаты
-линии к дифференциалу координаты 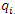 . Например, в цилиндрической системе координатными ρ- и z-линиями являются полупрямая и прямая соответственно, что влечет
. Например, в цилиндрической системе координатными ρ- и z-линиями являются полупрямая и прямая соответственно, что влечет 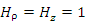 . Поскольку координатной
. Поскольку координатной 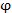 -линией является окружность радиуса ρ, то
-линией является окружность радиуса ρ, то 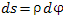 и
и