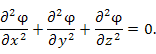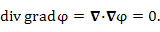Векторное поле A называется гармоническим (или лапласовым), если оно одновременно является безвихревым и соленоидальным:
Заметим, что гармоническое A поле является одновременно и потенциальным (см. "Безвихревое поле"), то есть может быть представлено в виде
Поэтому потенциал  векторного поля A удовлетворяет уравнению Лапласа: векторного поля A удовлетворяет уравнению Лапласа:
 Функции, удовлетворяющие уравнению Лапласа, называются гармоническими, поэтому потенциал любого потенциального поля прелставляет собой гармоническую функцию.
Функции, удовлетворяющие уравнению Лапласа, называются гармоническими, поэтому потенциал любого потенциального поля прелставляет собой гармоническую функцию.
 Скалярный квадрат
Скалярный квадрат 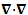 оператора набла называют лапласианом и обозначают символом оператора набла называют лапласианом и обозначают символом 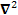 или или 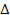 . В прямоугольной системе координат
В этих обозначениях уравнение Лапласа (1) принимает вид . В прямоугольной системе координат
В этих обозначениях уравнение Лапласа (1) принимает вид 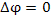 или или
|
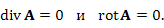

 векторного поля A удовлетворяет уравнению Лапласа:
векторного поля A удовлетворяет уравнению Лапласа:
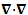 оператора набла называют лапласианом и обозначают символом
оператора набла называют лапласианом и обозначают символом 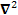 или
или 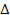 . В прямоугольной системе координат
. В прямоугольной системе координат


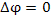 или
или